| okruh číslo 10 |
| 1. |
Definujte pojmy posloupnost, geometrická posloupnost. |
| 2. |
Dokažte.
V geometrické posloupnosti s kvocientem q platí pro každé přirozené číslo n : an = a1 qn-1.
|
| 3. |
Dokažte vzorec pro součet prvních n členů geometrické posloupnosti. |
| 4. |
Délky hran kvádru tvoří geometrickou posloupnost. Objem kvádru je 216 cm3. Součet délek hran vycházejících z jednoho vrcholu je 21 cm. Určete délky hran.
|
| 5. |
Délky stran a, b, c trojúhelníka ABC tvoří tři po sobě jdoucí členy geometrické posloupnosti. Jak jsou velké, je-li obvod trojúhelníka o = 42 cm a délka strany b = 8 cm?
|
| 6. |
Kratší úhlopříčka, strana a delší úhlopříčka kosočtverce mají délky, které tvoří tři po sobě jdoucí členy geometrické posloupnosti. Vypočítejte velikosti vnitřních úhlů kosočtverce.
|
| 7. |
Určete a1 a q v geometrické posloupnosti, ve které platí:
a1 + a3 + a5 = 105
 a2 + a4 = 50.
a2 + a4 = 50.
|
| 8. |
Předpokládejme, že an je geometrická posloupnost. Symbol N2 označuje množinu všech přirozených čísel počínaje číslem 2. Dokažte pravdivost následujícího výroku.
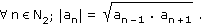
|
| 9. |
Určete číslo, které zvětšeno postupně o 7, 15, 27 dalo tři po sobě jdoucí členy geometrické posloupnosti. |
| 10. |
Určete ostrý úhel x tak, aby
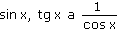
byly tři po sobě jdoucí členy geometrické posloupnosti.
|
| 11. |
Tři po sobě jdoucí členy aritmetické posloupnosti mají součet 21. Zmenší-li se prostřední číslo o 1 a zvětší-li se poslední člen o 6, vzniknou tři po sobě jdoucí členy posloupnosti geometrické. Určete členy obou posloupností.
|
| 12. |
Napište a vysvětlete definici limity posloupnosti (vlastní limity posloupnosti ). Potom dokažte některou z následujících vět:
V1 : Každá posloupnost má nejvýše jednu limitu.
V2 : Každá konvergentí posloupnost je omezená.
|
| 13. |
Pro které hodnoty q je geometrická posloupnost konvergentní? Vysvětlete pojem nekonečné geometrické řady a odvoďte její součet.
|
| 14. |
Co je to Sierpinského koberec? Vysvětlete tuto úlohu.

|
| 15. |
Dokažte správnost rovnosti.
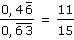
|
| 16. |
Vypočítejte součet:
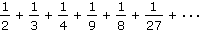
|
| 17. |
Vypočítejte limitu:
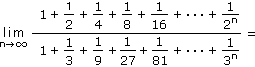
|
| 18. |
Řešte v R rovnici:
|