| okruh číslo 15 |
| 1. |
Vypočítejte (většinou zpaměti):
| a) |
 |
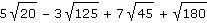b) |
 |
|
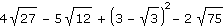| 2. |
Vypočítejte:
| a) |
 |
b) |
 |
|
| 3. |
Dokažte, že pro každou dvojici reálných čísel x, y platí:
|
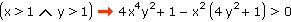
| 4. |
Vypočítejte (zpaměti), postup výpočtu zdůvodňujte:
|
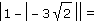
| 5. |
Porovnejte čísla C1 a C2:
| a) |
 |
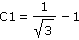b) |
 |
|
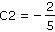| 6. |
Kolika způsoby umíte sestrojit úsečku délky  ?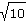
|
| 7. |
Definujte pojem komplexního čísla a operace sčítání a násobení komplexních čísel. Dále vysvětlete pojmy
 algebraický tvar komplexního čísla,
goniometrický tvar komplexního čísla.
|
| 8. |
Vysvětlete pojem izomorfního zobrazení množiny reálných čísel do množiny čísel komplexních. |
| 9. |
Vypočítejte součet, rozdíl, součin a podíl komplexních čísel z1, z2 (v uvedeném pořadí): z1 = 3 - i , z2 = 2 + 3 i. |
| 10. |
Zobrazte v Gaussově rovině všechna komplexní čísla z, pro která platí:
| a) |
| z - i | = 5 |
b) |
 |
| c) |
| z | > 3 |
d) |
 |
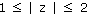| e) |
1 < | z - i | < 2 |
f) |
| z + z | = | z - z | |
| g) |
 |
h) |
| z . z - 2 | . | z . z - 4 | . | | z | - 4 | = 0 |
|
| 11. |
Dokažte, že pro libovolné komplexní číslo z platí: | z | = | z |. |
| 12. |
Vypočítejte a5, je-li dáno komplexní číslo a,
|
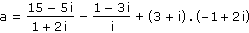
| 13. |
V oboru komplexních čísel řešte rovnice:
| a) |
x2 + 4 x + 5 = 0 |
b) |
x2 - 2 (1 + i) x + 2 i = 0 |
|
| 14. |
Řešte v R, potom v C:
| a) |
 |
b) |
 |
|
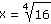| 15. |
Kolika způsoby dovedete vypočítat (1 + i)8 ? Který ze způsobů je efektivnější? |
| 16. |
Dokažte Moivreovu větu . |
| 17. |
Dokažte, že je dané číslo iracionální:
| a) |
 |
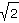b) |
 |
|
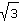