o1 o2 o3 o4 o5 o6 o7 o8 o9 Procvičte si úlohy z jednotlivých maturitních okruhů. Prostudujte si teorii, ovládejte definice a věty, které používáte. Dokažte svá tvrzení. hlavni strana okruhy o10 o11 o12 o13 o14 o15 o16 o17 o18 o19 o20 o21 o22 o23 o24 o25 o26 o27

Variace, permutace a kombinace (bez opakování), Pascalův trojúhelník školní rok 2008/2009

okruh číslo 20
1.	Definjte pojmy variace, kombinace a permutace (bez opakování).
2.	Řekněte (napište) definici čísla n! .
3.	Vyčíslete kombinační číslo .
4.	Zjednodušte následující výrazy: a) b)
5.	Určete všechny dvojice [x, y] N x N, pro které platí: .
6.	V množině přirozených čísel řešte soustavu: a) b)
7.	V oboru reálných číslech řešte danou rovnici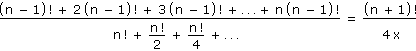
8.	Zapište základní vlastnosti kombinačních čísel, ukažte jejich platnost v Pascalově trojúhelníku a některou z vlastností dokažte. Potom dokažte následující vlastnost kombinačních čísel. Pro každou trojici nezáporných celých čísel p q r platí:
9.	Vyjádřete jediným kombinačním číslem : .
10.	Definujte pojem absolutní hodnoty reálného čísla. Jaký je geometrický význam absolutní hodnoty reálného čísla? Řešte v R následující rovnice a nerovnice: a) b) c) d) x! = 210 (x - 2)! e) (n!)2 - 7 n! + 6 = 0 f) g) h)
11.	Dokažte, že pro každé přirozené číslo n platí: .
12.	Zvětší-li se počet prvků o 1, zvětší se počet kombinací třetí třídy o 21. Kolik je dáno prvků?
13.	Kolik máme dáno prvků, jestliže variací třetí třídy z nich utvořených je pětkrát víc než variací druhé třídy ?
14.	Zvětší-li se počet prvků o 2, zvětší se počet permutací čtyřicetdvakrát. Určete původní počet prvků.
15.	Kolika přímkami můžeme spojit 10 bodů, jestliže a) žádné tři body neleží na jedné přímce, b) 5 z daných bodů leží na jedné přímce, jinak žádná trojice bodů na přímce neleží.
16.	Najděte vzorec pro částečný součet dané řady: a) 1 . 2 + 2 . 3 + 3 . 4 + ... + n . ( n + 1 ) + ... , b) 1 . 2 . 3 + 2 . 3 . 4 + ... + n . ( n + 1 ) . ( n + 2 ) + ... .
17.	Jsou dány dvě rovnoběžné přímky p, q. Na přímce p je dáno n různých bodů P1, P2, . . . ,Pn a na přímce q m různých bodů Q1, Q2, . . . , Qm. Určete počet všech trojúhelníků, jejichž vrcholy jsou v bodech přímky p a přímky q.
18.	Kolika způsoby lze na čtvercové šachovnici s 64 poli vybrat tři pole tak, aby všechna neležela v témže sloupci?
19.	Na maturitním večírku je 15 hochů a 12 děvčat. Určete, kolika způsoby z nich lze vybrat čtyři taneční páry.
20.	Určete, kolika způsoby může m chlapců a n dívek nastoupit do zástupu tak, aby: a) nejdříve stály všechny dívky a pak všichni chlapci, b) mezi žádnými dvěma chlapci nebyla žádná dívka ani mezi žádnými dvěma dívkami nebyl žádný chlapec, c) mezi žádnými dvěma chlapci nebyla žádná dívka.
21.	O telefonním čísle svého spolužáka si Vašek zapamatoval jen to, že je šestimístné, začíná sedmičkou, neobsahuje žádné dvě stejné číslice a je dělitelné 25. Určete, kolik telefonních čísel přichází v úvahu.
22.	K sestavení vlajky, která má být sestavena ze tří svislých různobarevných pruhů, jsou k dispozici látky barvy bílé, červené, modré, zelené, žluté a fialové. a) Určete počet vlajek, které lze z látek těchto barev sestavit. b) Kolik z nich má červený pruh? c) Kolik z nich má červený pruh uprostřed? d) Kolik jich nemá uprostřed zelený pruh?

© 2004 Milan Rieger - web design, grafika