| okruh číslo 11 |
| 1. |
Řešte početně i graficky soustavy lineárních rovnic v R2 . Při početním řešení ukažte všechny způsoby , kterými umíte soustavu rovnic řešit.
| a) |
x + y = 4
2 x - y = 5 |
b) |
x + y = 4
2 x + 2 y = 8 |
c) |
x + y = 4
2 x + 2 y = 6 |
|
| 2. |
Řešte v R2 soustavy lineárních rovnic s neznámými x, y a s reálným parametrem a:
| a) |
a x + 2 y = 10
4 x + y = 15 |
b) |
a x + y = a2
x + a y = 1 |
|
| 3. |
Řešte v R3 početně i graficky následující soustavy:
| a) |
12 x + 15 y + 20 z - 60 = 0
- 6 x + 3 y + 4 z - 24 = 0 |
b) |
12 x + 15 y + 20 z - 60 = 0
12 x + 15 y + 20 z - 120 = 0 |
c) |
x + y + z - 2 = 0
2 x - 3 y - z = 0 |
|
| 4. |
Rozložte na součet parciálních zlomků výraz:
|
| 5. |
Určete reálná čísla a, b tak, aby platila rovnost komplexních čísel:
a (4 + i) + b (5 - 2 i) = 2 + 7 i.
|
| 6. |
Řešte graficky i výpočtem soustavy rovnic:
| a) |
x2 = y
y - 5 = 0 |
b) |
x2 + y2 = 4
x + y = a (a je reálný parametr) |
c) |
x2 - y2 = 32
y - 2 x = 8 |
|
| 7. |
Řešte v R2 soustavy rovnic s neznámými x, y:
| a) |
x + y = 13
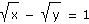 |
b) |
x2 + y2 - x y = 61
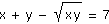 |
|
| 8. |
Řešte v R2 soustavy exponenciálních rovnic:
| a) |
2x . 3y= 24
2y . 3x= 54 |
b) |
yx = 16
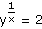 |
c) |
2x + 2 . 3x + y = 56
3 . 2x + 3x + y + 1 = 87 |
|
| 9. |
Řešte v R2 soustavy rovnic:
| a) |
2x . 4y = 32
log(x - y)2 = 2 log2 |
b) |
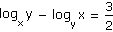
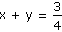 |
|
| 10. |
Řešte v R2 soustavy rovnic:
|
| 11. |
Řešte graficky v R2 soustavu:
| a) |
x + y - 1 > 0
 |
b) |
y > x2
x + y < 1 |
c) |
| x | + | y | = 2
| y | > 1 |
|
| 12. |
Řešte v R3 soustavy rovnic:
| a) |
2 x + 3 y - z = 18
3 x - 2 y + z = 8
x + 2 y + z = 24 |
b) |
x + y + z = 5
3 x - 2 y + z = 3
4 x - y + 2 z = 10 |
c) |
x + y + z = 4
x + y - z = 4 |
|
| 13. |
Řešte v R2 soustavu rovnic:
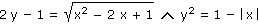
|
| 14. |
Graficky řešte v R2 soustavu nerovnic:
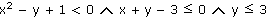
|
| 15. |
Narýsujte graf relace:
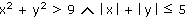
|
| 16. |
Vzdálenost dvou měst je 150 km. Rychlík ji ujede o 75 minut dříve než osobní vlak, protože ujede o 20 km za hodinu více než osobní vlak. Vypočtěte rychlost a dobu jízdy obou vlaků.
|
| 17. |
Rozdíl dvou přirozených čísel je 128, rozdíl jejich aritmetického a geometrického průměru je 16. Určete tato čísla.
|
| 18. |
Řešte v R4 soustavu rovnic:
| a) |
x1 + x2 - x3 - x4= 0
2 x1 - x2 + x3 + 2 x4= 1
x1 + 2 x2 - x3 + x4= 5
- x1 + x2 + x3 - x4= 4
|
b) |
x1 - 4 x2 + 2 x3 = 1
3 x1 - 7 x2 + x3 - 5 x4= - 6
x2 - x3 - x4= - 1
2 x1 - 3 x2 - x3 - 5 x4= - 7
|
|
| 19. |
Odvoďte algoritmus přímé (zpětné) substituce. |
| 20. |
Vysvětlete a ukažte na praktických úlohách (např. 18 a)) použití algoritmu GEM (Gaussova eliminační metoda) a JEM (Jordanova eliminační metoda). |
| 21. |
Řešte v oboru komplexních čísel soustavu nerovností, řešení vyznačte v rovině komplexních čísel:
|