| okruh číslo 1 |
| 1. |
Graficky řešte rovnici s reálnou neznámou x a reálným parametrem b: | x | + 3 = x + b. |
| 2. |
Určete množinu S všech funkcí, z nichž je každá určena rovnicí y = 2 x + g (g je celé číslo) a pro něž platí podmínka:
s
S,
x
<-2, 5> je s(x)
<-4, 15>.
|
| 3. |
Určete množinu S všech funkcí, z nichž je každá určená rovnicí y = a x + b (a
R, b
R) a pro něž platí zároveň tyto dvě podmínky:
a) uspořádaná dvojice [0, 2] patří každé z těchto funkcí,
b)
s
S,
x
<-1, 4) je s(x)
(-3, 5).
|
| 4. |
Napište rovnici lineární funkce, jejíž graf prochází bodem M [1, -4] rovnoběžně s přímkou 2 x - 5 y + 3 = 0. |
| 5. |
Graficky řešte v R rovnici: | x + 1 | - | x | + 3 | x - 1 | - 2 | x - 2 | = x + 2. |
| 6. |
Narýsujte grafy funkcí:
|
| 7. |
Napište rovnici inverzní funkce k funkci h. Načrtněte od ruky (ale přesně) grafy funkcí h a h-1.
h: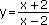 
|
| 8. |
Je ekvivalentní nerovnice x + 2 > 3 x - 5 a nerovnice (x + 2) (x - 5) > (3 x - 5) (x - 5)? Řekněte, jaké znáte ekvivalentní úpravy při řešení rovnic (nerovnic). |
| 9. |
Řešte rovnici (2 p - 1) x - 6 = p x s neznámou x
R a s parametrem p
R.
|
| 10. |
Řešte v C rovnici s neznámou x: (3 + i) (1 - i) x = 2 + i. |
| 11. |
Řešte v R rovnici:
|
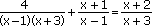
| 12. |
Kolika způsoby umíte řešit soustavu rovnic?
| a) |
x + 3 y + z = 5 |
b) |
2 x - y - z = 4 |
| 2 x + y + z = 2 |
3 x + 4 y - 2 z = 11 |
| 2 x + y + 5 z = - 7 |
3 x - 2 y + 4 z = 11 |
|
| 13. |
Určete, pro které hodnoty parametru a R je řešením dané soustavy rovnic jediná trojice kladných čísel.
| x + 3 y + z = 1 |
| 2 x - y - 3 z = 0 |
| 3 x + a y - 2 z = 3 |
|
| 14. |
Vysvětlete princip a použití lineární interpolace funkce f(x), známe-li [xi-1, f(xi-1)], [xi, f(xi)]. Použijte na následující úloze. Vypočítejte log 115,57, známe-li log 115,5 = 2, 06258 a log 115,6 = 2, 06296. |
| 15. |
Vysvětlete princip a použití Lagrangeovy interpolace [Ln(x)] a Newtonovy interpolace [Nn(x)] funkce. |
| 16. |
Vysvětlete pojem lineární závislosti (nezávislosti) určité skupiny vektorů a potom řešte následující úlohy:
a) Zjistěte, zda jsou body A[4, 7], B[5, 6], C[8, 10] vrcholy trojúhelníka.
b) Zjistěte, zda bod D leží v rovině ABC; D[4, 2, 4], A[0, 2, 6], B[1, 0, 2], C[1, -2, 0].
|
| 17. |
Vysvětlete pojmy "lineární kombinace vektorů" a "lineární závislost vektorů". Potom vysvětlete vztah mezi těmito pojmy. |
