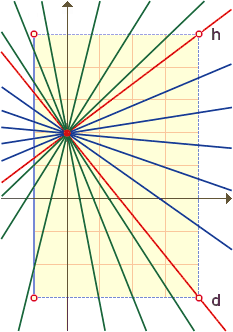
Při řešení úlohy vyjdeme z obrázku. Podmínkám nemohou vyhovovat přímky "zelené" a "červené", neboť není splněna podmínka b) úlohy. Budou vyhovovat všechny přímky "modré", které budou ležet mezi přímkami "červenými". Každá z uvedených přímek prochází bodem [0, 2].
V rovnici y = a x + b tedy známe b = 2. Přímka h je tedy určená rovnicí y = a x + 2 a navíc prochází bodem [4, 5]. Dosadíme-li do rovnice, dostaneme a = 0,75.
Podobně dostaneme pro přímku d, která prochází bodem [4, -3], a = -1,25.
Tedy řešením úlohy jsou všechny přímky, pro které platí
y = a x + 2, kde a (-1,25; 0,75).