| okruh číslo 9 |
| 1. |
Jak je posloupnost definovaná? Jak je definována aritmetická posloupnost? |
| 2. |
Napište, nakreslete a vysvětlete definici posloupnosti
 rostoucí,
klesající,
omezené shora,
omezené zdola,
omezené.
|
| 3. |
Dokažte, že je posloupnost an rostoucí;
 .
|
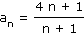| 4. |
Kdy je posloupnost určena rekurentně? Určete rekurentně posloupnost
| a) |
an = 2 n + 1 |
b) |
bn = n ( n + 1 ) |
|
| 5. |
Danou posloupnost vyjádřete vzorcem pro n - tý člen
| a) |
a1 = 5
an+1 = an + 4 |
b) |
a1 = 1
an+1 = an + 2 n + 1 |
|
| 6. |
Pro jaké hodnoty d je aritmetická posloupnost rostoucí, klesající, omezená, omezená zdola, omezená shora? Pravdivost některého svého výroku dokažte. |
| 7. |
Dokažte, že je posloupnost an = 5 n - 2 aritmetickou posloupností. |
| 8. |
Mezi kořeny rovnice x2 - 6 x + 8 = 0 vložte pět čísel tak, abychom dostali aritmetickou posloupnost. |
| 9. |
Dokažte vzorec pro součet prvních n - členů aritmetické posloupnosti. |
| 10. |
V aritmetické posloupnosti určete první člen a diferenci, víte-li, že platí:
| a) |
|
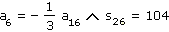
b) |
s5 = 60
s10 = 170
|
| c) |
s10 = s11 = 165 |
d) |
a4 + a5 = 4
a4 . a5 = - 5
|
|
| 11. |
V aritmetické posloupnosti je první člen a1 = 10 a diference d = - 2. Vypočítejte člen, který je roven jedné šestině součtu všech členů předchozích. |
| 12. |
Existuje konvexní n - úhelník, jehož nejmenší vnitřní úhel má velikost 126o a každý následující úhel je o 4o větší než úhel předcházející?
|
| 13. |
Vypočítejte součet všech trojciferných čísel dělitelných číslem 11.
|
| 14. |
Dokažte, že pro každé n přirozené je součet čísel n, n+1, n+2, n+3, ..., (3n-2) roven druhé mocnině nějakého přirozeného čísla. |
| 15. |
Délky stran pravoúhlého trojúhelníku tvoří tři po sobě jdoucí členy aritmetické posloupnosti. Jak jsou dlouhé, je-li obsah trojúhelníka 6 cm2? |
| 16. |
Najděte aritmetickou posloupnost, pro kterou platí:
Pro každé n přirozené je součet jejich prvních n členů roven trojnásobku druhé mocniny přirozeného čísla n.
|
| 17. |
Teploty Země přibývá směrem do jejího středu o 1o C na 33 metrů. Jaká je teplota v hloubce 1015 metrů, je-li v hloubce 25 m teplota 9o C? |
| 18. |
Velikosti vnitřních úhlů trojúhelníka tvoří tři po sobě jdoucí členy aritmetické posloupnosti. Určete je, je-li součet jejich kosinů roven 0,8. |
| 19. |
Pro která reálná čísla x jsou log 2, log(2x + 1), log(2x + 3) tři po sobě jdoucí členy aritmetické posloupnosti? |
| 20. |
Vypočítejte následující limity:
| a) |
 |
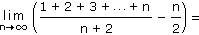b) |
 |
|
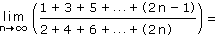