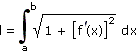| okruh číslo 13 |
| 1. |
Definujte pojem primitivní funkce a ukažte, že funkce F(x) = sin2x a G(x) = 1 - cos2x jsou primitivní funkce k téže funkci. Určete o jakou konstantu se funkce F(x) a G(x) liší. |
| 2. |
Pomocí tabulkových integrálů a většinou zpaměti vypočítejte:
|
| 3. |
Odvoďte tabulkové integrály: A B 2
| a) |
 |
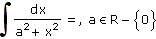b) |
 |
|
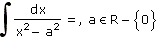| 4. |
Vypočítejte:
|
| 5. |
Z jaké věty vychází metoda per partes? |
| 6. |
Odvoďte rekurentní vzorce (rovnice) pro výpočet následujících integrálů:
|
| 7. |
Vypočítejte:
|
| 8. |
Integrujte:
| a) |
 |
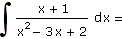b) |
 |
|
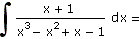| 9. |
Vypočítejte:
| a) |
 |
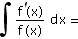b) |
 |
|
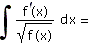| 10. |
Vypočítejte:
| a) |
 |
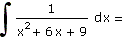b) |
 |
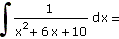c) |
 |
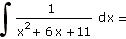| d) |
 |
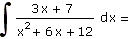e) |
 |
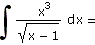f) |
 |
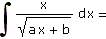| g) |
 |
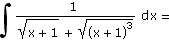h) |
 |
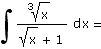i) |
 |
|
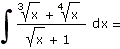| 11. |
Odvoďte vzorec pro výpočet objemu
 koule,
válce,
kužele.
|
| 12. |
Vypočítejte obsah obrazce omezeného křivkami:
| a) |
y = x2, 4 y = x2, y = 1 |
b) |
 |
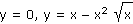| c) |
x = 1, y = ex, y = e-x |
d) |
y = x2 + 2, y = 0, x + y - 8 = 0 |
| e) |
y = x2 + 3, y = 2 x2 - 1 |
f) |
 |
|
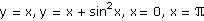| 13. |
Užitím určitého integrálu vypočtěte objem komolého rotačního kužele o rozměrech r1 = 6 cm , r2 = 4 cm , v = 5 cm. |
| 14. |
Odvoďte vzorec pro výpočet objemu
a) y2 + x - 4 = 0, x = 0, kolem osy y;
b) x2 - y2 = 4, y = - 2, y = 2, kolem osy y;
c) y = 1 - x2, y = x2, kolem osy x;
d) y = 0,5 x2 + 1, y = - x + 5, y = 0, x = 0, x = 4, kolem osy x.
|
| 15. |
Určete křivku, která prochází bodem A[- 4, 5] a jejíž směrnice v každém bodě x0 je 2 x0 + 14 . |
| 16. |
Vypočítejte délku křivky f(x) v intervalu <a, b> = <1, 2>. Pro výpočet délky křivky použijte vzorec l = ... .
| a) |
 |
|
 |
|
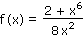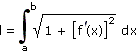