| okruh číslo 14 |
| 1. |
Která rovnice se nazývá kvadratická? Vysvětlete pojmy:
 ryze kvadratická rovnice,
kvadratická rovnice bez absolutního členu,
kvadratická rovnice v normovaném tvaru.
|
| 2. |
Vysvětlete postup řešení kvadratické rovnice s reálnými koeficienty v oboru - reálných čísel, komplexních čísel. |
| 3. |
Řešte nejdříve v R, potom v C rovnice:
| a) |
x2 - 7 x + 6 = 0 |
b) |
x2 - 4 x + 4 = 0 |
c) |
2 x2 + 3 x - 2 = 0 |
| d) |
3 x2 - 7 x = 0 |
e) |
3 x2 - 27 = 0 |
f) |
x2 - 2 x + 5 = 0 |
|
| 4. |
Řešte v C rovnici : x2 + ( 3 + 2 i ) x - 7 + 17 i = 0. |
| 5. |
Rozložte reálné číslo a na dva sčítance tak, aby byl jejich součin co největší. |
| 6. |
Které vztahy platí mezi kořeny a koeficienty kvadratické rovnice? |
| 7. |
Co víte o rozkladu kvadratického trojčlenu a x2 + b x + c = 0 (a, b, c jsou reálná čísla, a je různé od nuly) na součin kořenových činitelů? |
| 8. |
Určete všechny kvadratické rovnice jejichž
kořeny jsou čísla 3 a - 5,
dvojnásobným kořenem je číslo 0,4.
|
| 9. |
Je dána rovnice x2 - 2 x - 15 = 0. Sestavte kvadratickou rovnici v normovaném tvaru, jejíž kořeny jsou rovny druhým mocninám kořenů dané rovnice, aniž tuto rovnici řešíte. |
| 10. |
Je dána kvadratická rovnice a x2 + b x + c = 0, jejíž kořeny jsou x1, x2. Sestavte jednu kvadratickou rovnici, jejíž kořeny jsou čísla:
| a) |
 |
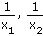b) |
 |
| |
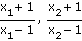předpoklad x1, x2 nenulová čísla |
|
předpoklad x1, x2 různá od 1 |
|
| 11. |
Řešte v R rovnice:
| a) |
 |
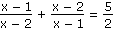b) |
(x - 2)3 = (x + 1)3 + 9 (x - 5) |
c) |
| x2 - 6 x + 8 | = 1 |
| d) |
 |
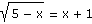e) |
 |
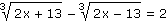f) |
 |
|
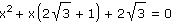| 12. |
Užitím vhodné substituce řešte v R následující rovnici
|
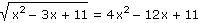
| 13. |
Řešte v R rovnici s neznámou x a s reálným parametrem m
(m - 1) x2 - 2 (m + 1) x + m - 2 = 0.
Stanovte, kdy má daná rovnice dva reálné různé kořeny oba kladné.
|
| 14. |
Určete definiční obor dané funkce:
| a) |
 |
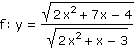b) |
 |
|
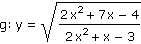| 15. |
Z listu lepenky tvaru čtverce o straně a se v rozích vyříznou stejně velké čtverce a ze zbylé části se slepí krabička. Jak velká musí být strana vyříznutého čtverce, aby objem krabičky byl co největší? |
| 16. |
Řešte v R rovnice:
|
| 17. |
Po řece se mezi dvěma místy A, B dopravuje nákladní lodí termínovaně náklad. Místo B leží ve vzdálenosti 24 km od místa A po proudu řeky. Rychlost proudu vody v řece je vp = 6 kmh-1. Jaká musí být vlastní rychlost lodi, aby její plavba z A do B a zpět (bez doby nakládání a vykládání nákladu) nebyla delší než 3 hodiny? |
| 18. |
Určete hodnotu reálného parametru a tak, aby obsah rovinného obrazce, který omezuje daná parabola y = a x2 - 3 a osa x byl 2. |
| 19. |
Určete hodnotu reálného parametru a tak, aby graf kvadratické funkce y = a x2 + x omezoval s osou x rovinný obrazec, jehož obsah je 24. |
| 20. |
Určete kvadratickou funkci tak, aby nabývala maxima pro x = 2, její graf procházel počátkem soustavy souřadné a graf této funkce spolu s osou x omezoval rovinný obrazec o obsahu 16. |
| 21. |
Řešte soustavu nerovnic s reálnými neznámými x, y a reálným parametrem p:
|
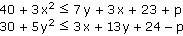
