| okruh číslo 23 |
| 1. |
Vyjádřete poloměr kružnice vepsané (kružnice opsané) pravoúhlému trojúhelníku, znáte-li velikosti jeho odvěsen.
|
| 2. |
V trojúhelníku ABC je dáno a = 10 cm, délka těžnice ta = 13 cm, 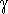 = 90o. Vypočítejte tb. = 90o. Vypočítejte tb. |
| 3. |
Jakými způsoby dovedete sestrojit úsečku u = 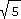 ? ? |
| 4. |
Daný pravoúhlý trojúhelník s odvěsnami a, b přeměňte na stejnoplochý čtverec. |
| 5. |
Dokažte Eukleidovy věty. |
| 6. |
Kruh o poloměru r rozdělte soustřednou kružnicí na dvě části, jejichž obsahy se sobě rovnají. |
| 7. |
Jsou dané soustředné kružnice s poloměry r1, r2 (r1 < r2). Sestrojte kružnici soustřednou, která rozděluje mezikruží na dvě části, jejichž obsahy se sobě rovnají. |
| 8. |
Sestrojte trojúhelník ABC, je-li dáno:
a) c = 8 cm, r (poloměr kružnice opsané), | SP | = 3 cm (SP je vzdálenost středu kružnice opsané od strany a). Určete podmínku řešitelnosti úlohy vzhledem k parametru r.
b) 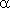 = 60o, a + b + c = 12 cm, vc = 3 cm. = 60o, a + b + c = 12 cm, vc = 3 cm.
c) a + b = 12 cm, 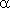 = 60o, = 60o, 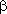 = 45o. = 45o.
d) a = 5 cm, va = 3 cm, 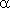 = 45o. = 45o.
|
| 9. |
Dokažte, že pro obsah S v každém trojúhelníku ABC platí (r označuje poloměr vepsané kružnice):
| a) |
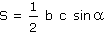 |
b) |
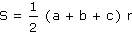
|
|
| 10. |
Určete velikost vnitřních úhlů trojúhelníka ABC, jestliže platí a : b = 2 : 3, 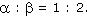 |
| 11. |
Vypočítejte šířku řeky, na jejímž jednom břehu byla změřena vzdálenost bodů A, B, | AB | = 50 m. Z koncových bodů úsečky AB je vidět bod C na druhém břehu řeky pod úhly 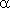 = 32o30’ a = 32o30’ a 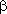 = 42o10’ vzhledem k úsečce AB. = 42o10’ vzhledem k úsečce AB. |
| 12. |
Na vrcholu kopce stojí rozhledna v metrů vysoká. Její patu a vrchol vidíme z určitého místa v údolí pod výškovými úhly 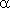 , , 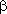 . Jak vysoko je vrchol kopce nad horizontální rovinou pozorovacího místa? . Jak vysoko je vrchol kopce nad horizontální rovinou pozorovacího místa? |
| 13. |
Z věže vysoké 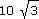 m a vzdálené od řeky 10 m se jevila šířka řeky v zorném úhlu 15o. Určete šířku řeky v tomto místě. m a vzdálené od řeky 10 m se jevila šířka řeky v zorném úhlu 15o. Určete šířku řeky v tomto místě. |
| 14. |
Jak velký je úhel 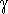 v trojúhelníku, o jehož stranách platí: v trojúhelníku, o jehož stranách platí:
| a) |
c2 = a2 + b2 + a b |
b) |
c2 = a2 + b2 - a b |
|
| 15. |
Silnice vedoucí po hrázi rybníka , má být po zrušení rybníka nahrazena přímou cestou. Její krajní body A, B jsou zaměřeny z bodu C pod úhlem 60o, přičemž | AC | = 421 m, | BC | = 233 m. Jak bude nová cesta dlouhá? |
| 16. |
Řešte trojúhelník, v němž je dáno a = 50, ta = 45, tb = 36. |