| okruh číslo 7 |
| 1. |
Vyslovte a symbolicky zapište definici hyperboly. Ukažte bodovou konstrukci hyperboly. |
| 2. |
V soustavě souřadné zobrazte hyperbolu:
| a) |
4 x2 - 9 y2 - 16 x - 18 y - 29 = 0, |
b) |
9 y2 - 4 x2 - 18 y - 16 x - 43 = 0 |
|
| 3. |
Vysvětlete pojem rovnoosé hyperboly. Potom dokažte následující větu:
"Asymtoty rovnoosé hyperboly jsou kolmé.".
|
| 4. |
Řešte v R danou rovnici výpočtem i graficky:
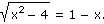 |
| 5. |
Vysvětlete a odvoďte souvislost:
| HYPERBOLA |
|
NEPŘÍMÁ ÚMĚRNOST |
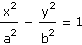 |
 |
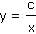 |
|
| 6. |
Dokažte větu:
"Součin vzdáleností libovolného bodu hyperboly b2 x2 - a2 y2 = a2 b2 od jejich asymptot je konstantní a rovná se číslu C."
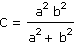 |
| 7. |
Narýsujte grafy následujících funkcí:
|
| 8. |
Napište rovnici inverzní funkce k funkci f. Dále načrtněte graf dané funkce a inverzní funkce do jednoho obrázku.
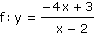 |
| 9. |
Je dána funkce g.
| a) |
Vypočítejte 1. a 2. derivaci funkce g v libovolném bodě definičního oboru. |
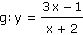
|
| b) |
Napište rovnici tečny a normály k funkci g v bodě T[-1, ?]. |
| c) |
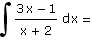 |
| d) |
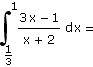 |
|
| 10. |
Napište rovnice tečen k hyperbole x2 - 4 y2 = 36 vedených z bodu M[6, 6]. |
| 11. |
Napište rovnici tečny ke křivce 9 x2 - 16 y2 - 54 x + 64 y - 127 = 0 v bodě T[8; -0,25]. |
| 12. |
Dokažte:
a) Asymptoty hyperboly nemají s hyperbolou žádný společný bod.
b) Rovnoběžka s asymptotou (různá od asymptoty) hyperboly protíná hyperbolu v právě jednom bodě.
|
| 13. |
Napište rovnici tečny k hyperbole 3 x2 - 4 y2 - 12 = 0, která:
a) je rovnoběžná s přímkou p: y = x + 2;
b) je kolmá k přímce h: y = x - 1.
|