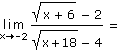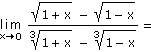o1 o2 o3 o4 o5 o6 o7 o8 o9 Procvičte si úlohy z jednotlivých maturitních okruhů. Prostudujte si teorii, ovládejte definice a věty, které používáte. Dokažte svá tvrzení. hlavni strana okruhy o10 o11 o12 o13 o14 o15 o16 o17 o18 o19 o20 o21 o22 o23 o24 o25 o26 o27

Funkce, limita funkce, derivace funkce, průběh funkce. školní rok 2008/2009

okruh číslo 4
1.	Definujte pojem funkce (reálné funkce jedné reálné proměnné). Definujte a vysvětlete základní vlastnosti funkcí (monotónnost, omezenost, sudost, lichost, periodičnost). Ukažte příklady funkcí, které danou vlastnost mají (nemají).
2.	Definujte, vysvětlete, nakreslete obrázky: a) pojem vlastní limita funkce ve vlastním bodě , b) pojem vlastní limita funkce v nevlastním bodě , c) pojem nevlastní limita funkce ve vlastním bodě , d) pojem nevlastní limita funkce v nevlastním bodě.
3.	Kolik může mít funkce f(x) v bodě a R limit? Své tvrzení dokažte.
4.	Načrtněte graf funkce , potom určete: a) D(f), H(f). b) c) Jaký je vztah mezi jednostrannými a oboustrannou limitou funkce v bodě? d) Definujte pojem funkce spojité v bodě (v intervalu <a, b> apod.).
5.	Vypočítejte následující limity: a) b) c) d) e) f) g) h) i) j) k) l) m) n)
6.	Vypočítejte následující limity: a) b) c) d)
7.	Určete všechny asymptoty funkce a určete limity dané funkce v bodech, ve kterých není definována.
8.	Napište definici derivace funkce f v bodě x0 a vysvětlete její geometrický a fyzikální význam. Potom pomocí definice derivace vypočítejte derivaci funkce v dodě x0 = 8.
9.	Narýsujte graf funkce f(x) = |x - 1| a určete: a) b) Je funkce f(x) spojitá v bodě 1? c) Má funkce f(x) derivaci v bodě 1? d) Formulujte větu o souvislosti spojitosti funkce v bodě a derivací funkce v tomto bodě. Své tvrzení dokažte. e) Načrtněte graf funkce f: y = sgn x. Vypočítejte f '(0+), f '(0-), f '(0).
10.	Formulujte pravidla (matematické věty) pro výpočet prvních derivací součinu konstanty a funkce, součtu (rozdílu) funkcí, součinu funkcí, podílu funkcí. Svá tvrzení dokažte.
11.	Vypočítejte první derivaci následující funkce: a) b) c) y = x2 cos x - tg x d) y = 3 cos2 x + sin x3 e) f)
12.	Formulujte větu o derivování inverzní funkce. Potom odvoďte derivaci některé z uvedených funkcí a) y = arcsin x b) y = arccos x c) y = arctg x d) y = arccotg x v libovolném bodě x0 definičního oboru funkce.
13.	Napište rovnici tečny a normály k funkci v bodě T[-2, ?]. Načrtněte graf funkce, bod dotyku, tečnu a normálu.
14.	Vyšetřete průběh funkce: a) y = x3 - 3 x + 2 b) y = x4 - 6 x2 + 8 c) d) y = ln(4 - x2) e) y = sin x + cos x f)
15.	Kolika způsoby dovedete řešit následující úlohu? Napište rovnice tečen ke kružnici x2 + y2 + 4 x - 4 y + 3 = 0 v jejich průsečících s osou x. Sestrojte kružnici a tečny.
16.	Průřez tunelu má tvar obdélníka s přilehlým půlkruhem. Obvod průřezu je 18 m. Při jakém poloměru půlkruhu bude obsah průřezu největší?
17.	Kolikrát je objem koule větší než objem největšího válce vepsaného téo kouli?
18.	Do elipsy 4 x2 + 9 y2 = 36 vepište obdélník maximálního obsahu. Určete jeho rozměry.
19.	Určete rozměry válcové nádoby s víkem tak, aby při objemu 2 litry měla tato nádoba minimální povrch.

© 2004 Milan Rieger - web design, grafika