| okruh číslo 17 |
| 1. |
Vysvětlete pojmy funkce, definiční obor funkce. Kdy říkáme, že je funkce prostá ve svém definičním oboru? Které z elementárních funkcí jsou funkcemi prostými (neprostými)?
|
| 2. |
Jak souvisí vlastnosti - funkce prostá, funkce rostoucí, funkce klesající? Formulujte jako matematické věty a některou z vět dokažte.
|
| 3. |
Vysvětlete pojem rovnosti funkcí. Rozhodněte, zda jsou si rovny dané funkce f, g:
| a) |
f(x) = 1
g(x) = sin2x + cos2x |
b) |
f(x) = x
g(x) = x2 . x-1 |
c) |
f(x) = sinx
g(x) = tg x . cos x |
|
| 4. |
Je dána funkce h. Určete všechna čísla c  R tak, aby platilo h(c+1) = h(0,5).
|
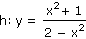
| 5. |
Jsou dány tři funkce:
| |
f(x) = x - 1 |
|
 |
|
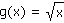h(x) = x + 3 |
Vytvořte složené funkce h1 až h4 a určete jejich definiční obory:
| a) |
h1(x) = g(h(f(x))) |
b) |
h2(x) = f(h(g(x))) |
| c) |
h3(x) = f(g(h(x))) |
d) |
h4(x) = h(g(f(x))) |
|
| 6. |
Určete hodnotu parametru a R tak, aby pro funkci h(x) = a x + 3 platilo h(h(2)) = 17.
|
| 7. |
U daných složených funkcí určete funkci vnější a funkci vnitřní:
| a) |
 |
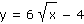b) |
y = log2 x |
| c) |
 |
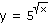d) |
y = log2 x - 4 log x |
| e) |
 |
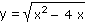f) |
y = log x2 |
| g) |
 |
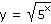h) |
y = (x2 + 1)3 |
|
| 8. |
Dokažte:
a) funkce g: y = 4 x – 7 je rostoucí v R,
b) funkce g: y = - 3 x + 5 je klesající v R.
|
| 9. |
Které z daných funkcí jsou sudé (liché) v definičním oboru?
| a) |
y = x |
b) |
y = 4 x |
c) |
y = | x | |
| d) |
y = x3 |
d) |
y = cos x |
f) |
y = x2 |
| g) |
y = log x |
h) |
y = 2x |
i) |
 |
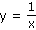| j) |
 |
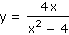k) |
 |
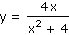l) |
 |
|
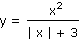| 10. |
Za předpokladu, že znáte graf funkce y = f(x), načrtněte graf funkce
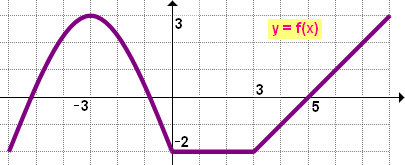
| a) |
y = f(x) + 2 |
b) |
y = f(x + 2) |
c) |
y = f(x - 1) |
| d) |
y = f(x - 1) - 3 |
e) |
y = 2 f(x) |
f) |
y = 0,5 f(x) |
| g) |
y = - f(x) |
h) |
y = - f(2x) |
i) |
y = | f(x) | |
| j) |
y = f(| x |) |
k) |
y = f(| - x |) |
l) |
y = | f(| x |) | |
|
| 11. |
Určete ( zpaměti ) definiční obor následujících funkcí:
| a) |
y = log (x - 3) |
b) |
y = log x2 |
c) |
 |
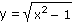| d) |
 |
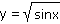e) |
 |
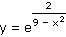f) |
y = log logx |
|
| 12. |
Definujte logaritmus a formulujte pravidla (věty) pro logaritmování součinu, podílu a mocniny.
|
| 13. |
Určete, pro které hodnoty reálného parametru a jsou funkce f, g rostoucí (klesající):
| a) |
 |
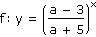b) |
 |
|
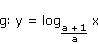| 14. |
Vysvětlete pojem inverzní funkce. Jakou vlastnost musí mít funkce f, aby k ní existovala funkce inverzní? |
| 15. |
Jak se nazývají inverzní funkce k funkcím lineárním, mocninným, exponenciálním, logaritmickým, goniometrickým? |
| 16. |
Napište rovnici inverzní funkce (relace) k následujícím funkcím:
| a) |
y = 4 x - 3 |
b) |
 |
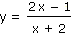c) |
y = 3x - 1 |
| d) |
y = log (x + 2) |
e) |
y = x2 - 1 |
f) |
y = sin x |
|
| 17. |
Do jedné soustavy souřadné načrtněte grafy následujících dvou funkcí:
| a) |
y = log2x, y = 2x |
b) |
y = x2,  |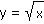
c) |
y = x3,  |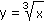
|
| 18. |
Určete, pro které hodnoty reálného parametru a jsou funkce f, g rostoucí (klesající):
| a) |
1000 x2 = xlog x |
b) |
 |
|
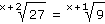| 19. |
Narýsujte graf některé z cyklometrických funkcí:
 y = arcsin x,
y = arccos x
y = arctg x,
y = arccotg x.
|
| 20. |
Ukažte odvození derivace funkce y = arcsin x (i dalších cyklometrických funkcí) pomocí věty o derivování inverzní funkce. |
| 21. |
Jaké zobrazení dostaneme složením dvou stejnolehlostí HS, h=0,25 a KS, k=2 v tomto pořadí? Ukažte prakticky na zobrazení bodu. Co dostaneme složením daných stejnolehlostí v opačném pořadí? |
| 22. |
Do jednoho obrázku načrtněte grafy těchto funkcí:
y = cos x,
y = 2 cos x
y = cos 2x,
y = cos (-2x),
y = 2 cos 2x.
Které z těchto funkcí jsou funkcemi složenými?
|
| 23. |
Derivujte funkci:
| a) |
y = (x2 + 2 x + 2)3 |
b) |
y = 3 cos2 x + 2 sin3 x + cos x3 + sin x2 |
| c) |
 |
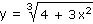d) |
 |
|
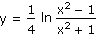| 24. |
Integrujte:
|
