| okruh číslo 18 |
| 1. |
Definujte pojem absolutní hodnoty reálného čísla. Jaký je geometrický význam absolutní hodnoty reálného čísla? Řešte v R následující rovnice a nerovnice:
| a) |
| x - 2 | = 3 |
b) |
| x + 2 | = - 3 |
c) |
| x + 3 |  1 1 |
| d) |
| x - 2 |  2 2 |
e) |
| x - 1 |  0 0 |
f) |
| x - 1 |  0 0 |
| g) |
| x - 2 | < 0 |
h) |
| x - 2 | > 0 |
i) |
| x - 1,5 | < 1,75 |
|
| 2. |
Definujte pojem absolutní hodnoty komplexního čísla. Jaký je geometrický význam absolutní hodnoty komplexního čísla? Řešte v oboru komplexních čísel následující rovnice a nerovnice:
| a) |
| x - 2 | = 3 |
b) |
| x - 2 |  3 3 |
c) |
| x - 2 |  3 3 |
|
| 3. |
Definujte vlastní limitu funkce ve vlastním bodě, vysvětlete na příkladu dané funkce v bodě a = 2
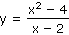
|
| 4. |
Dokažte, že pro každou dvojici reálných čísel x, y platí:
| a) |
| x . y | = | x | . | y | (zobecněte) |
b) |
| x | = | - x | |
| c) |
| x | + | y | ? | x + y | (zobecněte) |
d) |
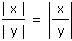
(předpokládáme y různé od nuly) |
|
| 5. |
Pro jaká reálná čísla x platí následující rovnosti?
| a) |
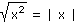 |
b) |
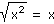 |
|
| 6. |
Řešte v R výpočtem následující nerovnice:
| a) |
| 2 x - 4 | + | 3 x + 6 | - | 5 x - 2 |  8 - 4 x 8 - 4 x |
b) |
| x + 2 | - 2 | 2 x + 4 |  | 3 x - 1 | | 3 x - 1 | |
| c) |
| 3 - | 2 - x | |  2 x 2 x |
d) |
| x - 3 | . | x - 2 | . | x + 4 | > 0 |
| e) |
| x2 - 9 x + 14 | . | x + 3 |  0 0 |
f) |
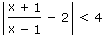 |
| g) |
| | x + 1 | - | x - 1 | | < 1 |
h) |
| x2 - 4 |  5 5 |
|
| 7. |
Řešte graficky v R rovnici 2 x + 1 – 2 | x + 1 | + | x – 3 | = | x |. Potom ukažte grafické řešení následujících nerovnic:
| a) |
2 x + 1 – 2 | x + 1 | + | x – 3 |  | x | | x | |
b) |
2 x + 1 – 2 | x + 1 | + | x – 3 | < | x | |
| c) |
2 x + 1 – 2 | x + 1 | + | x – 3 |  | x | | x | |
d) |
2 x + 1 – 2 | x + 1 | + | x – 3 | > | x | |
|
| 8. |
Načrtněte v soustavě souřadné grafy následujících relací:
a) | | x | - | y | | = 1,
b) | x | + | y | = 4,
c) 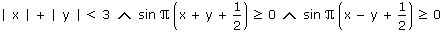 , ,
d) 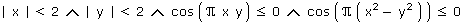 . .
|
| 9. |
Řešte graficky v R x R následující soustavy nerovnic (rovnic):
a) 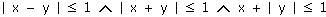 , ,
b) 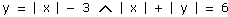 . .
|
| 10. |
Ukažte postup efektivního rýsování grafu následující funkce f(x):
| a) |
f(x) = |||| x - 1 | - 2 | - 3 | - 4 | |
b) |
f(x) = ||||| x | - 1 | - 1 | - 1 | - 1 | |
| c) |
f(x) = |||| x | - 1 | - 2 | - 3 | |
d) |
f(x) = ||||| x | + 1 | - 2 | + 3 | - 4 | |
| e) |
f(x) = | 1 - | 2 - | 3 - | x |||| |
f) |
f(x) = | 3 - | 2 - | 1 - | x |||| |
|
| 11. |
Vypočítejte:
| a) |
| (7 + i) . (4 - 3 i ) | = |
b) |
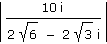 |
c) |
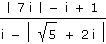 |
|