Řešení úlohy 8c) - grafy jednotlivých relací jsou kreslené ve čtvercové síti se stranou čtverce 0,5.

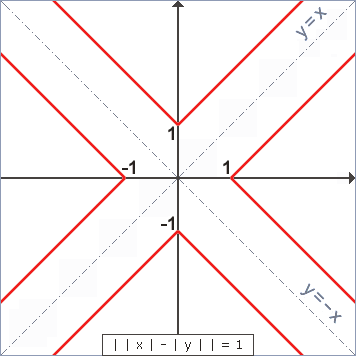
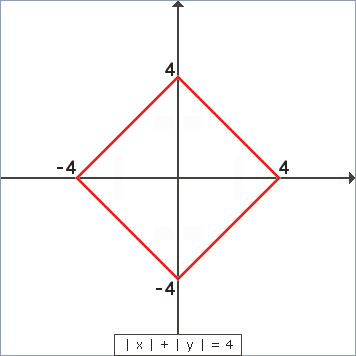
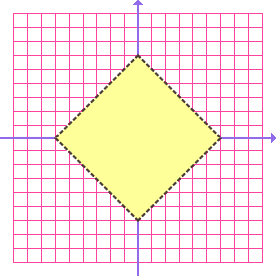
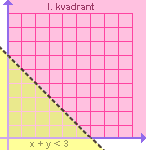
Graf relace | x | + | y | < 3.

I. případ: Předpokládejme, že x 0 a y 0. Tedy uspořádané dvojice [x, y] leží v I. kvadrantu. Na základě předpokladu platí |x| = x a |y| = y. Pro všechny dvojice z I. kvadrantu tedy musí platit x + y < 3, tedy y < - x + 3. Malý obrázek dokumentuje graf relace v I. kvadrantu. ...

Pro každou dvojici reálných čísel x, y platí (k je libovolné celé číslo):


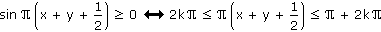
Po příslušných úpravách dostáváme:

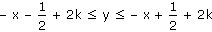
Po dosazení "šikovných" hodnot za k dostaneme:
k = -4: - x - 8,5 y - x - 7,5
k = -3: - x - 6,5 y - x - 5,5
k = -2: - x - 4,5 y - x - 3,5
k = -1: - x - 2,5 y - x - 1,5
k =  0: - x - 0,5 y - x + 0,5
k =  1: - x + 1,5 y - x + 2,5
k =  2: - x + 3,5 y - x + 4,5
k =  3: - x + 5,5 y - x + 6,5
k =  4: - x + 7,5 y - x + 8,5

Pro každou dvojici reálných čísel x, y platí (k je libovolné celé číslo):


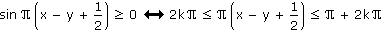
Po příslušných úpravách dostáváme:

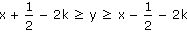
Po dosazení "šikovných" hodnot za k dostaneme:
k = -4: x + 8,5 y x + 7,5
k = -3: x + 6,5 y x + 5,5
k = -2: x + 4,5 y x + 3,5
k = -1: x + 2,5 y x + 1,5
k =  0: x + 0,5 y x - 0,5
k =  1: x + 1,5 y x - 2,5
k =  2: x - 3,5 y x - 4,5
k =  3: x - 5,5 y x - 6,5
k =  4: x - 7,5 y x - 8,5