|
|
|
| 4. |
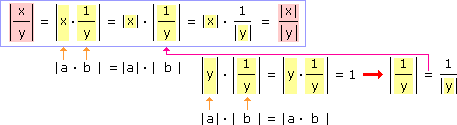
Dokažte, že pro každou dvojici reálných čísel x, y platí: a) | x . y | = | x | . | y | (zobecněte) |
|
Nejdříve si připomeňme definici pojmu absolutní hodnota reálného čísla. 1. část důkazu (uvažujeme všechny dvojice čísel x, y z I. kvadrantu)

|
|
|
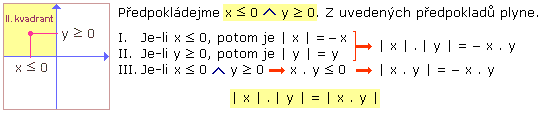
2. část důkazu (uvažujeme všechny dvojice čísel x, y z II. kvadrantu)
|
|
|
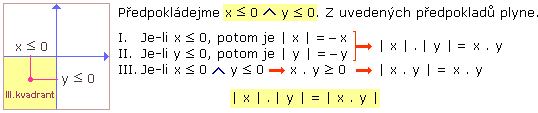
3. část důkazu (uvažujeme všechny dvojice čísel x, y z III. kvadrantu)
|
|
|
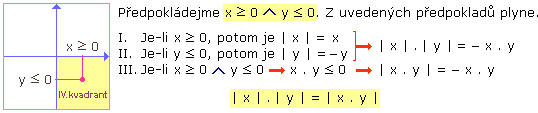
4. část důkazu (uvažujeme všechny dvojice čísel x, y ze IV. kvadrantu)
|
|
|
zobecnění

|
|
| b) Dokažte, že pro každé reálné číslo x platí: | x | = | - x | | |
|
1) Předpokládejme, že x je nezáporné reálné číslo, tedy x |
|
| c) Dokažte, že pro každou dvojici reálných čísel x, y platí: | x | + | y | ? | x + y | (zobecněte) | |
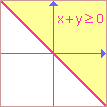
Vztah doplníme relací. |
|
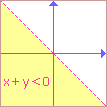
2) Předpokládejme, že x + y < 0
|
|
|
zobecnění
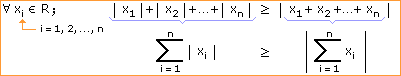
|
|
|
d) Dokažte, že pro každou dvojici reálných čísel x, y platí (předpokládáme y různé od nuly):
|
|
|
V dokazovní můžeme postupovat podobně jako při dokazování rovnosti | x . y | = | x | . | y |. K důkazu můžeme také použít tuto (již dokázanou) rovnost takto: |
|
| Gymnázium V. Hlavatého, Poděbradova 661, 440 62 Louny |
| © 2004 Milan Rieger - webdesign, grafika |