o1 o2 o3 o4 o5 o6 o7 o8 o9 Procvičte si úlohy z jednotlivých maturitních okruhů.
Prostudujte si teorii, ovládejte definice a věty, které používáte.
Dokažte svá tvrzení. 		hlavni strana
okruhy
o10 o11 o12 o13 o14 o15 o16 o17 o18
o19 o20 o21 o22 o23 o24 o25 o26 o27
Vzájemné polohy útvarů
školní rok 2008/2009
okruh číslo 24
 1. Zjistěte, zda leží dané body v jedné přímce:
a) A[1, 2], B[-3, 10], C[0, 4];
b) A[0, 3, 2], B[2, 1, 6], C[-1, 4, 0];
c) A[-2, 5, 3], B[1, 4, 5], C[2, 1, -1].
 2. Zjistěte, zda polopřímka x = 3 + t, y = 1 - t, t < 0 protíná úsečku AB (A[-2, 0], B[2, 8]). Určete souřadnice průsečíku.
 3. Určete velikost neznámých konstant m, n tak, aby přímka (3 - m) x + 12 y + 2 - n = 0 splývala s přímkou
2 x - 3 y + 2 = 0.
 4. Zjistěte, zda leží dané body A, B, C, D v rovině:
a) A[2, -3, 1], B[6, -10, 2], C[-3, -1, -5], D[1, -8, -4];
b) A[1, 0, 1], B[2, 2, -1], C[4, 6, -2], D[1, 2, 5].
 5. Určete hodnoty parametru m tak, aby byly přímky a, b různoběžné.
a: x = m + 2 t, t R
y = - 2 + 3 t
z = 6 - 4 t		 b: x = 5 + s, s R
y = 1 - 4 s
z = - 4 + s
 6. Najděte společný bod tečen v průsečících kružnice x2 + y2 - 3 x - 4 y - 6 = 0 s přímkou x = 4. Řešte graficky i výpočtem.
 7. Jaké podmínky musí splňovat koeficienty a, b, c, aby rovnice a x + b y + c = 0 byla rovnicí:
a) přímky rovnoběžné s osou x, ale různé od ní;
b) osy x;
c) přímky rovnoběžné s osou y, ale různé od ní;
d) osy y;
e) přímky procházející počátkem.
 8. Určete vzájemnou polohu paraboly 10 x - y2 = 0 a přímky x - y + c = 0, kde c je reálný parametr.
 9. Určete vzájemnou polohu rovin , . Řešte výpočtem i graficky.
a) : 2 x + y + z - 6 = 0
: 2 x + y + z - 4 = 0 		b) : 2 x + y + z - 6 = 0
: 2 x + y + 6z - 12 = 0
10. Určete průsečík přímky p:   s rovinou : x + y - z + 2 = 0.
11. Řešte graficky i výpočtem (zpaměti) vzájemnou polohu útvarů x2 + y2 = 4, y2 = 3 x.
12. Určete průsečíky přímky KL s krychlí ABCDEFGH. Vyznačte viditelnost přímky KL.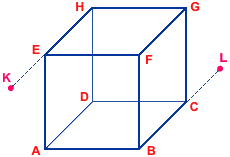
13. V krychli ABCDEFGH sestrojte řez rovinou KLM.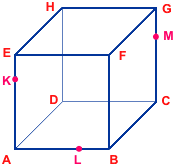
14. Sestrojte řez hranolu ABCDEFGHIJ rovinou KLM.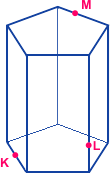
15. Určete vzájemnou polohu přímky x = 3 - t, y = -1 + t, t R a hyperboly 9 x2 - 4 y2 = 36.
 
© 2004 Milan Rieger - web design, grafika