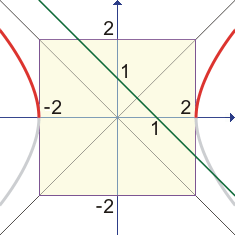
Grafické řešení je patrné z obrázku. Levá strana dané rovnice je "červenou" částí rovnoosé hyperboly o rovnici x² - y² = 4. Pravá strana dané rovnice je přímka určená rovnicí y = 1 - x (na obrázku je vyznačena zelenou barvou). Tato přímka je rovnoběžná s asymtotou y = - x. Kdyby měla daná rovnice řešení, musela by se přímka y = 1 - x protínat v alespoň jednom bodě s červenou částí hyperboly. Průnikem "zelené" přímky a "červené" části hyperboly je prázdná množina. Daná rovnice tedy nemá v R řešení.

Řešení výpočtem začneme určením definičního oboru dané rovnice. Protože musí platit x² - 4 0 (tedy ekvivalentně (x - 2) . (x + 2) 0), je definičním oborem dané rovnice množina ( - , - 2> <2, + ). Rovnici umocníme na druhou, dostaneme x² - 4 = 1 - 2 x + x². Dále dostáváme x = 2,5. Číslo 2,5 leží v definičním oboru dané rovnice, ale to nám ještě nezaručuje to, že je kořenem dané rovnice. Při řešení iracionálních rovnic děláme vždy zkoušku (v průběhu řešení rovnice používáme neekvivalentní úpravu, umocňujeme rovnici na druhou).
Po dosazení a výpočtu levé strany rovnice dostaneme L_(2,5) = 1,5. Dosazení do pravé strany a následný výpočet dá výsledek P_(2,5) = - 1,5. Vidíme rozdílné výsledky ("zkouška nevyšla") na pravé a levé straně, tedy rovnice nemá v R řešení.