Okruh 10 - příklad 12

1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - 11 - 12 - 13 - 14 - 15 - 16 - 17 - 18

12.

Napište a vysvětlete definici limity posloupnosti (vlastní limity posloupnosti ). Potom dokažte některou z následujících vět:
V1: Každá posloupnost má nejvýše jednu limitu.
V2: Každá konvergentí posloupnost je omezená.

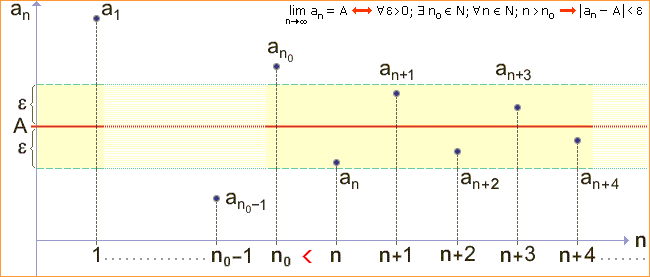
1) Definice vlastní limity (A R ) posloupnosti a_n

2) Definice nevlastní limity (+ ) posloupnosti a_n

3) Definice nevlastní limity (- ) posloupnosti a_n

4) V1: Každá posloupnost má nejvýše jednu limitu.
Větu dokážeme sporem. Budeme předpokládat, že má posloupnost a_n alespoň dvě různé limity. Tyto limity si označíme například A, B (tedy A, B jsou dvě různá reálná čísla). Podle definice limity musí k libovolnému > 0 současně

1) existovat n₀₁

N; n > n₀₁

A -

< a_n < A +

;
2) existovat n₀₂

N; n > n₀₂

B -

< a_n < B +

.
zvolíme n₀ = maximum (n₀₁; n₀₂)
musí tedy pro libovolné n

N; n > n₀ platit A -

< a_n < A +

B -

< a_n < B +

;
dále musí platit | A - B | = | A - B + a_n - a_n | = |(A - a_n) + (a_n - B)|

|A - a_n| + |a_n - B| <

= 2

;
pokud bychom zvolili

(tedy | A - B | = 2

), dostaneme se do sporu, neboť lze z této volby odvodit
vztah | A - B | < 2

. Předpoklad důkazu sporem tedy nemůže platit (nemůže platit, že posloupnost a_n má
alespoň dvě různé limity), tedy musí platit věta V1 - posloupnost má nejvýše jednu limitu.

Posloupnost může mít tedy buď právě jednu limitu, nebo nemá limitu žádnou. Tato věta platí i pro nevlastní limity.

5) V2: Každá konvergentí posloupnost je omezená.

Důkaz této věty je zřejmý z prvního obrázku. Bylo by dobré si při důkazu obrázek nakreslit (nebo si jej představit) a pak jej pouze komentovat.

Chceme dokázat oboustrannou omezenost posloupnosti a_n, což podle definice znamená dokázat pravdivost výroku

D, H

N; D

a_n

Budeme předpokládat, že posloupnost a_n je konvergentní. Podle definice musí platit:

N; n > n₀ platí A -

< a_n < A +

Víme tedy, že počínaje členem a_n₀+1 jsou všechny další členy posloupnosti (je jich nekonečně mnoho) shora omezené konstantou A +

a zdola konstantou A -

. Podívejme se na všechny členy posloupnosti a₁, a₂, ..., a_n₀. Těch je konečný počet. Z konečného počtu čísel mohu vybrat vždy číslo minimální i maximální.

D = minimum (minimum(a₁, a₂, ..., a_n₀); A -

); H = maximum (maximum(a₁, a₂, ..., a_n₀); A +

).
Existují tedy reálné konstanty D, H takové, že pro libovolné přirozené číslo n platí D

a_n

H.
Tedy posloupnost a_n je omezená a daná věta platí.

Gymnázium V. Hlavatého, Poděbradova 661, 440 62 Louny