Okruh 10
1 -
2 -
3 -
4 -
5 -
6 -
7 -
8 -
9 -
10 -
11 -
12 -
13 -
14 -
15 -
16 -
17 -
18
| |||||||||
| 18. | Řešte v R rovnici:
|
||||||||
|
Řešení rovnice 18 a)
Máme řešit rovnici  . Musí být x
 0 a současně x 4/3. Na levé straně rovnice je nekonečná geometrická řada, ve které je a1 = 1 a kvocient q = 2/x. Aby se jednalo o konvergentní nekonečnou geometrickou řadu, musí platit  .
Pokud x splňuje podmínku konvergence, bude součet na levé straně rovnice roven  . Dostaneme rovnici  . Řešením této rovnice dostaneme rovnici x2 - 7 x + 6 = 0, která má kořeny x = 1 nebo x = 6. Z čísel 1, 6 vyhovuje dané rovnici pouze číslo 6.
Řešení rovnice 18 b)
Definičním oborem dané rovnice je množina kladných reálných čísel. Rozepíšeme-li levou stranu rovnice, dostaneme  V okrouhlé závorce je nekonečná geometrická řada, ve které je a1 = 1 a q = 0, 5. Řada je konvergentní a její součet je 2. Dostáváme rovnici 2 log x = 2, tedy log x = 1. Této rovnici vyhovuje číslo 10. 
Řešení rovnice 18 c)
Po rozepsání levé strany rovnice dostaneme 2x + 22x + 23x + ... = 1. Na levé straně rovnice je nekonečná geomatrická řada s prvním členem a1 = 2x a kvocientem q = 2x. Podmínkou konvergence této řady je 2x < 1. Této podmínce vyhovují pouze záporná reálná čísla. Danou rovnici můžeme potom zapsat ve tvaru
Řešení rovnice 18 d)
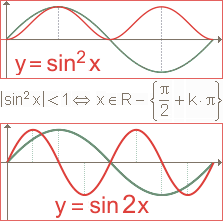Máme řešit rovnici 1 + sin2x + sin4x + sin6x + ... = 2 tg x. Vlevo je nekonečná geometrická řada, pro kterou platí a1 = 1, q = sin2x. Aby bylo možné určit součet 1 + sin2x + sin4x + sin6x + ..., musí platit | sin2 x | < 1 (viz orázek). 
|
|||||||||
| Gymnázium V. Hlavatého, Poděbradova 661, 440 62 Louny |
| © 2004 Milan Rieger - webdesign, grafika |