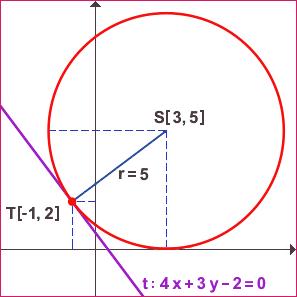
Grafické řešení úlohy s hledanou tečnou ukazuje názorně obrázek. Výpočtem lze řešit úlohu třemi způsoby.

1) Souřadnice vektoru ST (4, 3) jsou v obecné rovnici tečny a x + b y + c = 0 pořadě koeficienty a, b. Máme tedy 4 x + 3 y + c = 0. Absolutní člen (c) v této rovnici určíme z požadavku "bod T musí ležet na tečně t". Řešením této rovnice dostaneme c = - 2.

2) Využijeme znalosti o rovnici tečny ke kružnici
(x - m)² + (y - n)² = r² v bodě T[x₀, x₀]. Rovnice takové tečny je
(x - m).(x₀ - m) + (y - n).(y₀ - n) = r².
Stačí tedy do této rovnice dosadit příslušné hodnoty.

3) Derivací dané imlicitní funkce v bodě dotyku T dostaneme směrnici tečny ke kružnici v bodě T (k_t = - 4/3). Stačí dosadit příslušné hodnoty do rovnice tečny t: y - y₀ = k_t . (x - x₀).