| |
Libovolný bod X [x, y] roviny má od dané přímky vzdálenost |x - 8|. Vzdálenost bodu X od bodu K je rovna
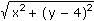 . Dle zadání úlohy má platit:
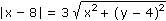
8 . (x + 1)2 + 9 (y - 4)2 = 72
Tato rovnice je středovou rovnicí elipsy.
S [- 1, 4], a = 3, b =  .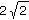
Jestliže budeme uvažovat libovolný bod X [x, y] uvedené elipsy, lze postupnými úpravami rovnice dojít až k rovnici
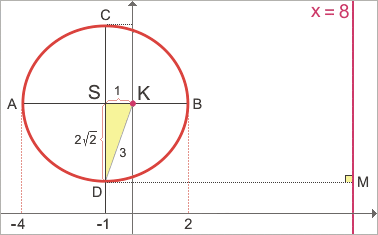
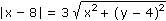. To ale znamená, že bod X má od přímky x = 8 třikrát větší vzdálenost než od bodu K[0, 4]. Lze tedy tvrdit, že hledanou množinou bodů je množina všech bodů elipsy. Při pohledu na obrázek je například vidět, že pro bod X = D platí
|DM| = 3 . |KD| apod. Podobné úlohy vždy vyžadují obrácení postupu. Musíme ukázat, že libovolný bod ležící na nalezené křivce má požadovanou vlastnost.
|
Okruh 3 