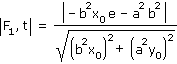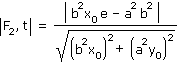Okruh 3
1 -
2 -
3 -
4 -
5 -
6 -
7 -
8 -
9 -
10 -
11 -
12 -
13 -
14 -
15 -
16 -
17 -
18 -
21
| |
| 21. | Dokažte, že součin vzdáleností ohnisek elipsy od libovolné tečny elipsy je konstantní. Určete tuto konstantu. |
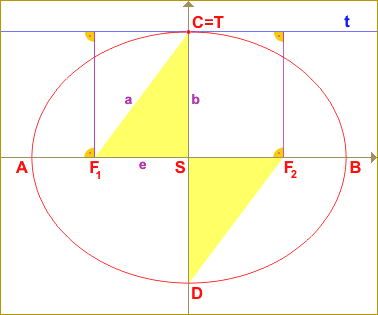
Na prvním obrázku je vidět jedna z poloh tečny t elipsy b2 x2 + a2 y2 = a2 b2, kdy bod C splývá s bodem dotyku T[x0, y0]. Z této polohy tečny plyne, že součin vzdáleností ohnisek F1, F2 od této tečny je roven konstantě b2. To je první odhad hledané konstanty. Tím ovšem řešení úlohy nemůže končit, je to pouze dobrý začátek. Stejně to dopadne i v případě tečny k elipse v bodě D. |
|
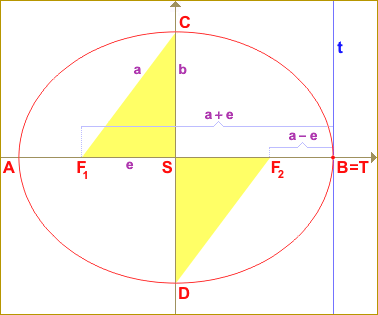
Na druhém obrázku vidíme tečnu k elipse v bodě B. Opět platí - součin vzdáleností ohnisek F1, F2 od tečny t je roven konstantě b2. Podobně i v bodě A. To samozřejmě není konec důkazu, neboť tečen k elipse b2 x2 + a2 y2 = a2 b2 v bodě elipsy T je nekonečně mnoho. Ale tušíme, jakou hodnotu bude mít hledaná konstanta. |
|
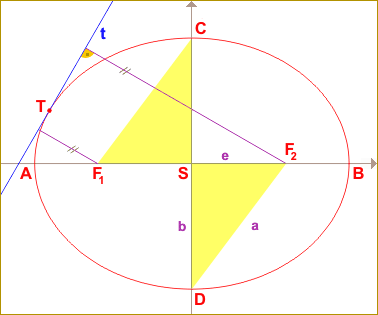
Na třetím obrázku vidíme obecnou úlohu. Pracujeme tedy s elipsou b2 x2 + a2 y2 = a2 b2, bod dotyku tečny t a elipsy označíme T. Souřadnice bodu T si označíme x0, y0. Protože bod T leží na elipse, musí pro jeho souřadnice platit rovnice b2 x02 + a2 y02 = a2 b2. F1[-e, 0], F2[e, 0]. Tečna t je určena rovnicí b2x0x + a2y0y - a2b2 = 0. |
|
| Gymnázium V. Hlavatého, Poděbradova 661, 440 62 Louny |
| © 2004 Milan Rieger - web design, grafika |