| KATEGORIE Z9 |
| (54. ročník matematické olympiády, školní rok 2004/2005, úlohy I. kola - domácího kola) |
| Z9 - I - 1 |
Dvojmístné číslo se nazývá exkluzivní, jestliže má následující vlastnost:
Číslice exkluzivního čísla navzájem vynásobíme, po přičtení součtu všech číslic exkluzivního čísla k předchozímu výsledku získáme toto exkluzivní číslo. Například 79 je exkluzivní, neboť 79 = 7 . 9 + (7 + 9). Najděte všechna exkluzivní čísla.
|
| (P. Tlustý) |
| Z9 - I - 2 |
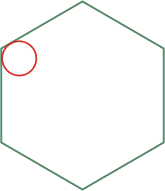
Uvnitř pravidelného šestiúhelníka o straně délky
cm se pohybuje kruh o průměru 1 cm tak, že se stále dotýká obvodu pravidelného šestiúhelníku. Vypočítejte obsah té části šestiúhelníku, která nemůže být nikdy překryta pohybujícím se kruhem.
|
 |
| (M. Dillingerová) |
| Z9 - I - 3 |
|
Kolika způsoby lze vybrat 7 čísel z množiny {1, 2, ..., 8, 9} tak, aby jejich součet byl dělitelný třemi?
|
| (P. Tlustý) |
| Z9 - I - 4 |
|
Jsou dánz kruh a čtverec se stejným obsahem. Do daného kruhu vepíšeme čtverec, do daného čtverce vepíšeme kruh. Který z vepsaných obrazců má větší obsah?
|
| (M. Volfová) |
| Z9 - I - 5 |
|
Pan Sudý měl sudý počet oveček, pan Lichý lichý počet oveček. Počet všech oveček dohromady tvořil trojmístné číslo, které mělo všechny číslice stejné. Každé ovečce pana Sudého se narodily tři ovečky, každé ovečce pana Lichého dvě ovečky. Jednoho dne však vlk zadávil tři ovečky panu Sudému. Teď má pan Sudý stejně velké stádo jako pan Lichý. Kolik oveček měl původně každý z chovatelů?
|
| (L. Hozová) |
| Z9 - I - 6 |
|
Pět dětí postupně říká: "Včera bylo pondělí." "Dnes je čtvrtek." "Pozítří bude pátek" "Zítra bude sobota." "Předevčírem bylo úterý." Pokud byste věděli, kolik z dětí lhalo, hned by bylo jasné, který den právě je. Určete, který je tedy den?
|
| (Š. Ptáčková) |
| © 2004 Milan Rieger - web design, grafika |