54. ročník MO 2004/2005, kategorie Z5

KATEGORIE Z5

(54. ročník matematické olympiády, školní rok 2004/2005, úlohy I. kola - domácího kola)

Z5 - I - 1

Vendelín zavřel do bedny všechna dvojmístná čísla, která při dělení pěti dávají zbytek 3, avšak na jedno z nich zapomněl. Když čísla v bedně správně sečetl, dostal součet 911. Na které číslo zapomněl?

(L. Hozová)

Z5 - I - 2

Andulka a Maruška měly sraz přesně v 17:30 před kinem. Andulka si myslela, že jí jdou hodinky o 4 minuty napřed, ale ve skutečnosti se jí zpožďovaly o 8 minut. Maruška si myslela, že se jí hodinky o 8 minutt zpožďují, ale šly jí o 4 minuty napřed. Kdy která z dívek přišla na sraz, jestlie si obě myslely, že přišly přesně v 17:30?

(Š. Ptáčková)

Z5 - I - 3

Tři bratři princové šli na mnohohlavého draka. První princ mu levou rukou usekl polovinu hlav a pravou rukou ještě další dvě. Totéž udělali se zbylými hlavami druhý a třetí princ. Potom drak padl. Na kolikahlavého draka se princové vydali?

(Š. Ptáčková)

Z5 - I - 4

Na obrázku je mnohoúhelník složený z jedenácti stejných čtverečků.
a) Zjisti jeho obvod, jestliže víš, že jeden malý čtvereček má obvod 20 cm.
b) Které dva čtverečky mnohoúhelníku je nutno ubrat, aby vznikl nový mnohoúhelník s co největším obvodem?
Namaluj aspoň jedno řešení.

(S. Bednářová)

Z5 - I - 5

Hrací kostka má puntíky rozmístěny tak, že jejich součet na protilehlých stěnách je vždy 7. Kostka na obr. 1 stojí na stěně s jedním puntíkem, takže na podložce zanechá otisk 1. Když převalíme kostku doprava na stěnu se dvěma puntíky, zanechá na podložce otisk 2. Když pak převalíme kostku směrem k sobě, zanechá otisk 3. Při tomto valení dostaneme stopu na obr. 2. Součet čísel této stopy je 6. Jestliže výchozí postavení kostky je na obr. 1,
a) jaký bude součet na stopě na obr. 3?
b) Jak bude vypadat stopa, na níž je součet 22?

(L. Hozová)

Z5 - I - 6

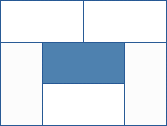
Ivanka si staví z kostek komíny. Všechny kostky jsou stejné a mají rozměry 1 cm, 1 cm a 2 cm. Teď postavila jednopatrový dutý komín z pěti kostek na plošše 12 cm² (viz obr.). Rozhodla se ale, že postaví dutý komín na ploše 36 cm² z 260 takových kostek. Jaký největší komín mohla postavit, jestliže jí žádná kostka nezbyla a komín byl nahoře rovný?

(Š. Ptáčková)