54. ročník MO 2004/2005, kategorie Z8

KATEGORIE Z8

(54. ročník matematické olympiády, školní rok 2004/2005, úlohy I. kola - domácího kola)

Z8 - I - 1

Pořadové číslo dne v měsíci je smutné, protože v jistém roce nebylo ani jednou nedělí. Jaké číslo to bylo a na který den v týdnu připadl v tom roce Nový rok?

(M. Volfová)

Z8 - I - 2

Slimák lezl po čtvercové síti a zanechal za sebou stopu (viz obr. 1). Čísla pod sítí a vedle ní udávají počet navštívených čtverečků v daném řádku či sloupci. Na obr. 2 určete dráhu slimáka, víte-li, že nikdy nevlezl dvakrát do stejného čtverečku a že nikdy nelezl šikmo.

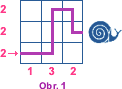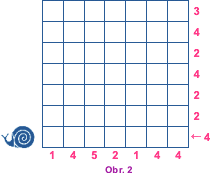(Š. Ptáčková)

Z8 - I - 3

O lichoběžníku LICH (LI || CH) víme, že LC

HI, |

ILC | = |

IHC | a aritmetický průměr délek jeho základen je 8 cm. Vypočítejte obsah tohoto lichoběžníku.

(S. Bednářová)

Z8 - I - 4

Kolik je mezi čísly 1, 2, 3, ..., 999, 1 000 takových, která nejsou dělitelná žádným z čísel 2, 3, 4, 5?

(M. Volfová)

Z8 - I - 5

Alenka sestavovala "hlemýždí ulitu" z pravoúhlých rovnoramenných trojúhelníků jako na obrázku. Použila k tomu co nejvíc trojúhelníků, ale žádné dva se nepřekrývaly.
a) Z kolika trojúhelníků byla ulita sestavena?
b) Jaký je obsah největšího trojúhelníku, je-li odvěsna nejmenšího z nich dlouhá 1 cm?

(M. Raabová)

Z8 - I - 6

Archeologové vykopali papyrus se zvláštní tabulkou s výřezem ve tvaru "Z" (viz obr.). Jde zřejmě o talisman. Měl zajímavou vlastnost: zakroužkujeme-li libovolných pět čísel tak, aby v každém sloupci i řádku bylo zakroužkované právě jedno, a těchto pět čísel sečteme, dostaneme vždy stejný součet. Pokuste se zrekonstruovat tento talisman, tzn. doplňte čísla na prázdná místa

(S. Bednářová)