| KATEGORIE B |
| (54. ročník matematické olympiády, školní rok 2004/2005, úlohy I. kola - domácího kola) |
| B - I - 1 |
|
Určete všechny dvojice (a, b) reálných čísel, pro které má každá z rovnic
x2 + a x + b = 0, x2 + (2a + 1) x + 2b + 1 = 0
dva různé reálné kořeny, přičemž kořeny druhé rovnice jsou převrácené hodnoty kořenů první rovnice.
|
| E. Kováč |
| B - I - 2 |
|
Je dán rovnoběžník ABCD. Přímka vedená bodem D protíná úsečku AC v bodě G, úsečku BC v bodě F a polopřímku AB v bodě E tak, že trojúhelníky BEF a CGF mají stejný obsah. Určete poměr |AG| : |GC|.
|
| T. Jurík |
| B - I - 3 |
|
Na stole leží k hromádek o 1, 2, 3, ... , k kamenech, kde k > 2. V každém kroku vybereme tři libovolné hromádky na stole, sloučíme je do jedné a přidáme k ní jeden kámen, který na stole dosud neležel. Jestliže po několika krocích vznikne jediná hromádka, není výsledný počet kamenů dělitelný třemi. Dokažte.
|
| J. Zhouf |
| B - I - 4 |
|
Označme V průsečík výšek a S střed kružnice opsané trojúhelníku ABC, který není rovnostranný. Pokud má vnitřní úhel při vrcholu C velikost 60o, je osa úhlu ACB osou úsečky VS. Dokažte.
|
| J. Zhouf |
| B - I - 5 |
V oboru reálných čísel řešte rovnici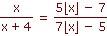 , kde , kde
 označuje největší celé číslo, jež nepřevyšuje číslo x (tzv. dolní celá část reálného čísla x). označuje největší celé číslo, jež nepřevyšuje číslo x (tzv. dolní celá část reálného čísla x).
|
| J. Šimša |
| B - I - 6 |
|
Do kružnice k o poloměru r jsou vepsány dvě kružnice k1, k2 o polměru 0,5r, jež se vzájemně dotýkají. Kružnice l se vně dotýká kružnic k1, k2 a s kružnicí k má vnitřní dotyk. Kružnice m má vnější dotyk s kružnicemi k2 a l a vnitřní dotyk s kružnicí k. Vypočtěte poloměry kružnic l a m.
|
| L. Boček |
| © 2004 Milan Rieger - web design |