| KATEGORIE Z9 |
| (52. ročník matematické olympiády, školní rok 2002/2003, úlohy I. kola - domácího kola) |
| Z9 - I - 1 |
|
Nahraďte hvězdičky v čísle 683*** vhodnými číslicemi tak, aby výsledné šestimístné číslo bylo dělitelné 7, 8, 9.
|
| (Tlustý) |
| Z9 - I - 2 |
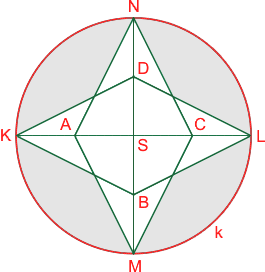
Vypočítej obsah šedé plochy vyznačené na obrázku, pokud víte, že KL a MN jsou dva navzájem kolmé průměry kružnice k(S,6cm) a body A, B, C a D jsou po řadě středy úseček KS, MS, LS a NS.
|
 |
| (Bednářová) |
| Z9 - I - 3 |
|
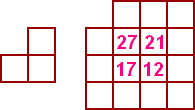
Do tabulky na obrázku byla doplněna čísla tak, že součet trojice v každém "trojčtverečku" (bez otáčení) byl stejný. Určete součet čísel v tabulce.
|
 |
| (Dillingerová) |
| Z9 - I - 4 |
|
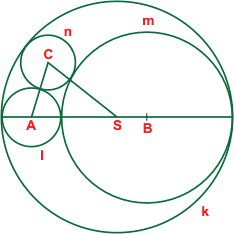
Na průměru kružnice k(S, r) leží dvou kružnic l(A, r1) a m(B, r2), které se vzájemně dotýkají a dotýkají se i kružnice k. Navíc uvnitř kružnice k leží ještě n(C, r3), která se dotýká kružnic k, l a m (obr.). Světlana si myslí, že obvod trojúhelníku ASC je větší než průměr kružnice k. Má pravdu? Proč?
|
 |
| (Volfová) |
| Z9 - I - 5 |
|
Průměrný věk žáka naší školy je 10 let, průměrný věk učitelů je 54 let, průměrný věk žáků a učitelů dohromady je 12 let. Určete průměrný počet žáků ve třídě této školy, pokud víte, že učitelé učí průměrně 21 hodin týdně a děti mají v průměru 24 vyučovacích hodin týdně.
|
| (Bednářová) |
| Z9 - I - 6 |
|
Martin chodí ze školy obvykle pěšky. Pokud jede na kole, jeho průměrná rychlost se zvýší o 10 km/h a doba, kterou mu trvá cesta, se zkrátí o 15 minut. Přijede-li pro něj otec autem, průměrná rychlost se zvýší šestkrát a čas se zkrátí o 20 minut. Jak daleko to má Martin do školy (trasa do školy je ve všech případech stejná)?
|
| (Dillingerová) |
| © 2004 Milan Rieger - web design, grafika |


