| KATEGORIE Z7 |
| (52. ročník matematické olympiády, školní rok 2002/2003, úlohy I. kola - domácího kola) |
| Z7 - I - 1 |
|
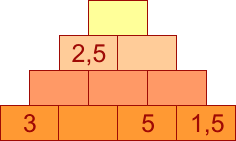
Doplň do obrázku čísla tak, aby na každé cihličcee, která není ve spodní vrstvě, byl napsaný aritmetický průměr všech čísel z tmavých cihliček, než je ona.
|
 |
| (Bednářová) |
| Z7 - I - 2 |
|
Zuzka, Martin, Jakub a Petra hráli kuličky. Když hra skončila, měla Zuzka o 4 kuličky méně než byla polovina všech kuliček, Martin měl pětinu všech kuliček a ještě 6 navíc, Jakub třikrát méně než Zuzka a Petra o jednu kuličku méně než Jakub. Které z dětí mělo na konci hry nejméně a které nejvíce kuliček?
|
| (Bednářová) |
| Z7 - I - 3 |
|
V pravidelném pětiúhelníku ABCDE o straně délky 5 cm označme M průsečík úseček AC, BD. Vypočítej velikost úsečky AM a velikost úhlu AMB.
|
| (Bednářová) |
| Z7 - I - 4 |
Určete nejmenší přirozené číslo n, pro něž je součin
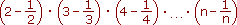 ,
dělitelný stem. ,
dělitelný stem.
|
| (Ptáčková) |
| Z7 - I - 5 |
|
Rozděl rovnostranný trojúhelník na čtyři shodné útvary. Jeden z nich odeber a zbytek opět rozděl na čtyři shodné útvary. Najdi alespoň jedno řešení a narýsuj je.
|
| (Hozová) |
| Z7 - I - 6 |
|
V době dovolené paní Veselé patnáctkrát pršelo, ale nikdy ne celý den. Když pršelo dopoledne, bylo odpoledne jasno. Pršelo-li odpoledne, bylo v tomto dni dopoledne jasno. Jasno bylo 9 dopolední a 8 odpolední. Jak dlouho trvala dovolená paní Veselé?
|
| (Bednářová) |
| © 2004 Milan Rieger - web design, grafika |
