52. ročník MO 2002/2003, kategorie Z5

KATEGORIE Z5

(52. ročník matematické olympiády, školní rok 2002/2003, úlohy I. kola - domácího kola)

Z5 - I - 1

Doplňte do tabulky přirozená čísla tak, aby v každém jejím bílém políčku byl součin příslušných čísel z jejího šedého záhlaví.

(Bednářová)

Z5 - I - 2

Na obrázku je znázorněn pětiúhelník a šestiúhelník s vrcholy v mřížkových bodech čtvercové sítě. Urči obsah šestiúhelníka, víš-li, že pětiúhelník má obsah 7,5 cm².

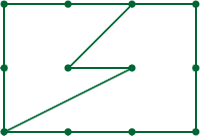(Bednářová)

Z5 - I - 3

Nevill opět zapomněl heslo pro vstup do věže. Profesorka McGonagallová mu však prozradila, že:
- heslo se skládá ze tří různých písmen,
- dobře se vyslovuje, protože v něm nejsou dvě souhlásky vedle sebe,
- všechna písmena hesla najdete ve jméně vedoucího učitele Slizolinu - "Snape".
Po vyzkoušení třetiny všech hesel, vyhovujících těmto podmínkám, se vstup do věže otevřel. Kolik hesel Nevill vyzkoušel?

(Bednářová)

Z5 - I - 4

Doplň do obrázku čísla tak, aby na každé cihličce byl napsán součet všech čísel z tmavších cihliček, než je ona.

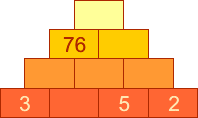(Bednářová)

Z5 - I - 5

Míša měl včera o 15 samolepek víc než Pavel. Dnes však ale 17 svých vyměnil za 9 Pavlových a dlaších 7 vyměnil za 13 Oldových. Pavel kromě těch devíti, které vyměnil za 17 Míšových, vyměnil ještě 11 svých za 6 Láďových. Který z chlapců má teď víc samolepek, Míša nebo Pavel? O kolik?

(Bednářová)

Z5 - I - 6

O mnohoúhelníku načrtnutém na obrázku víme, že jej přímka p přesně dělí na dvě shdoné části. Jeho strany měří 3 cm, 4 cm, 5 cm a 6 cm. Jaký obvod může mít tento mnohoúhelník?

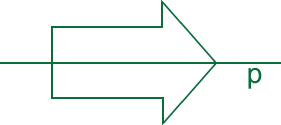(Bednářová)