Okruh 19
2 -
3 -
8 -
9 -
10 -
11 -
12 -
13 -
14 -
15 -
16 -
17 -
18 -
19 -
20 -
21
| |
| 18. | Jak se dokazuje rovnost dvou množin, například M = N ? |
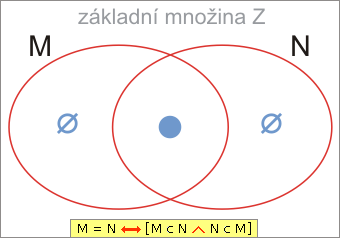
Důkaz rovnosti množin M, N se skládá ze dvou částí, které musí platit současně. Proměnnou x označme libovolný prvek základní množiny Z.
1) Jestliže x
Příklad:  M
x N (tedy dokazujeme M
N).2) Jestliže x N
x M
(tedy dokazujeme N
M).Máme dokázat, že pro libovolné podmnožiny A, B, C základní množiny Z platí [ A  ( B
 C )
] = [ ( A
B)
( A
C) ].
1) Dokážeme
[ A
pro libovolný prvek x základní množiny Z platí: ( B
C )
] [ ( A
B )
( A
C ) ]
x [ A
( B C ) ]
x A  x ( B C )
x A (
x B 
x C )
[ ( x A
x B )
( x A
x C ) ]
[ x A B
x A C ]
x [ ( A B )
( A C ) ]
2) Dokážeme
[ ( A
pro libovolný prvek x základní množiny Z platí: B )
( A
C ) ]
[ A
( B
C ) ]
x [ ( A B )
( A C ) ]
[ x A B
x A C ]
[ ( x A
x B )
( x A
x C ) ]
x A (
x B
x C )
x A
x ( B C )
x [ A
( B C ) ]
V důkazu se použije definice množinových operací průnik množin a sjednocení množin, dále poznatky z výrokové logiky.
Podívejte se na
tautologii výrokové logiky, která byla použita v uvedeném důkazu.
|
|
| Gymnázium V. Hlavatého, Poděbradova 661, 440 62 Louny |
| © 2004 Milan Rieger - webdesign, grafika |