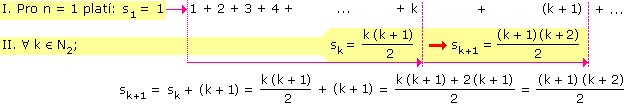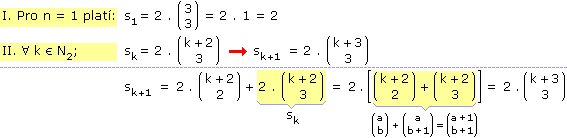Okruh 19    2 - 3 - 8 - 9 - 10 - 11 - 12 - 13 - 14 - 15 - 16 - 17 - 18 - 19 - 20 - 21
13. Najděte vzorec pro částečný součet sn následující řady, vzorec přesně zapište a dokažte jej:
a) 1 + 2 + 3 + 4 + ...
 

Jedná se o aritmetickou posloupnost (řadu), ve které je a1 = 1 a diference d = 1. Částečný součet této řady je součtem prvních n členů aritmetické posloupnosti, tedy pro libovolé přirozené číslo n platí:

Důkaz provedeme úplnou matematickou indukcí.
  b) 1 + 3 + 5 + 7 + ...
 

Jedná se o aritmetickou posloupnost (řadu), ve které je a1 = 1 a diference d = 2. Částečný součet této řady je součtem prvních n členů aritmetické posloupnosti, tedy pro libovolé přirozené číslo n platí: sn = n2.
Důkaz provedeme úplnou matematickou indukcí.

   I. Pro n = 1 platí: s1 = 1
   II. k N2; sk = k2    sk+1 = (k + 1)2
   sk+1 = sk + (2k + 1) = k2 + 2 k + 1 = (k + 1)2
Důkaz schématicky: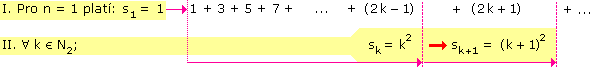
  c) 1 . 2 + 2 . 3 + 3 . 4 + ...
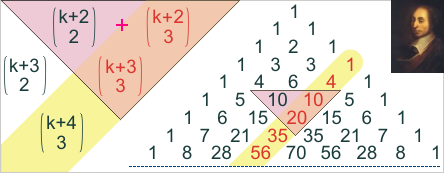
  Pascalův trojúhelník

Zkusíme vypočítat několik prvních členů posloupnosti částečných součtů a pak uvidíme dále:
s1 = 2 = 2 . 1
s2 = 8 = 2 . 4
s3 = 20 = 2 . 10
s4 = 40 = 2 . 20
s5 = 70 = 2 . 35
s6 = 112 = 2 . 56
s7 = 168 = 2 . 84, ...
Je zřejmé, že tučně označená čísla jsou vyčíslenými kombinačními čísly (viz obrázek). Několik prvních členů posloupnosti částečných součtů si můžeme přepsat pomocí kombinačních čísel, formulujeme domněnku

Důkaz provedeme úplnou matematickou indukcí.
  d)
 

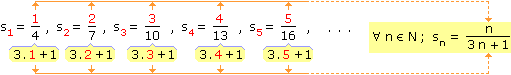Vypočítáme několik prvních členů posloupnosti částečných součtů, potom zobecníme a dokážeme. Důkaz provedeme úplnou matematickou indukcí.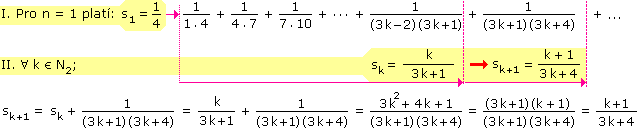

Gymnázium V. Hlavatého, Poděbradova 661, 440 62 Louny
© 2004 Milan Rieger - webdesign, grafika