| |
Z obrázku je parametrické vyjádření kružnice zřejmé (bod X[x, y] je libovolným bodem kružnice k, která má střed S v počátku soustavy souřadné a má poloměr r). Po umocnění (/2) obou rovnic a jejich sečtení dostaneme rovnici x2 + y2 = r2 . (sin2
+
cos2
), což je středová rovnice kružnice x2 + y2 = r2.
Pokud by se jednalo o kružnici posunutou do bodu S[m, n], budou parametrické rovnice takové kružnice
x=m+r.cos
,
y=n+r.sin
,
kde úhel alfa leží v uvedeném intervalu. Každá z těchto rovnic se dá zapsat v následujícím tvaru
x - m = r . cos
,
y - n = r . sin
.
Po umocnění (/2) obou rovnic a jejich sečtení dostaneme středovou rovnici kružnice (x - m)2 + (y - n)2 = r2.
Výhodou parametrických rovnic kružnice je to, že umožňují matematické vyjádření částí kružnice. Úhel je parametrem libovolného bodu X kružnice k.
|
| |
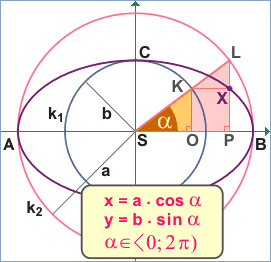
Pro souřadnice libovolného bodu X[x, y] elipsy platí:
1) Souřadnice x bodu X je stejná jako x-ová souřadnice bodu L. Bod L leží na kružnici k2, jejíž poloměr je a. Pro daný úhel alfa tedy platí (viz pravoúhlý trojúhelník SPL): x = a . cos .
2) Souřadnice y bodu X je stejná jako y-ová souřadnice bodu K. Bod K leží na kružnici k1, jejíž poloměr je b. Pro daný úhel alfa tedy platí (viz pravoúhlý trojúhelník SOK): y = b . sin .
Pokud elipsu posuneme tak, že S[m, n] a zachováme rovnoběžnost hlavní osy elipsy s osou x, dostaneme x-m=a.cos
, y-n=b.sin . Po umocnění (/2) obou rovnic, vynásobením první rovnice číslem b2, vynásobením druhé rovnice číslem a2 a sečtení rovnic dostaneme rovnici b2 (x - m)2 + a2 (y - n)2 = a2 b2. Položíme-li a = b = r, dostaneme středovou rovnici kružnice v posunutém tvaru. Úhel je parametrem libovolného bodu X elipsy.
|
Okruh 3