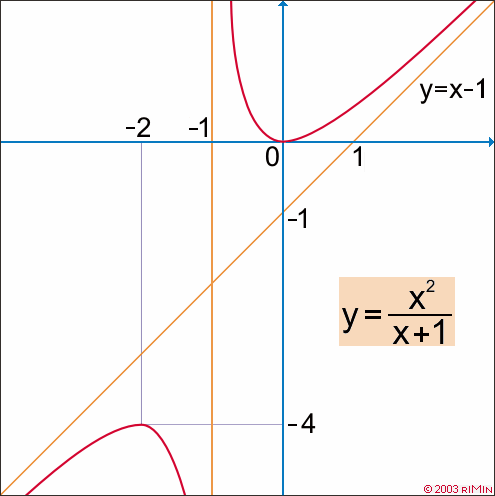|
Poznámky:
-
Víme, že operace dělení reálných čísel není komutativní. Prakticky to znamená, že výsledek dělení 4 : 2 je jiný, než výsledek dělení 2 : 4. Přejděme od konkrétních čísel k výrazům (s jednou reálnou proměnnou x) a proveďme náledující přiřazení:
4
 x2
x2
2
 x + 1.
x + 1.
Proměnné y přiřadíme následující podíl x2 :
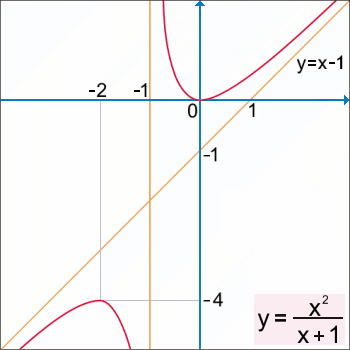
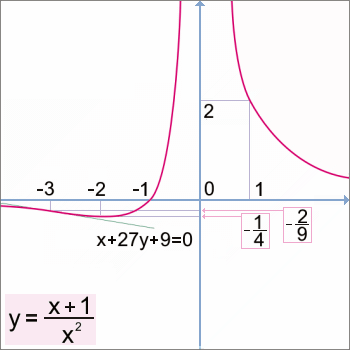
(x + 1). Dostáváme funkci, jejíž graf známe a derivaci máme již vypočítanou. Podílu 2 : 4 potom bude odpovídat "nová" funkce y = (x + 1) : x2. Na následujícím obrázku porovnejte rozdíly v grafech obou funkcí. Dále vypočítejte oběma způsoby derivaci této funkce a porovnejte derivace původní funkce a funkce "nové".
- Důležitý příklad
Proveďme následující přiřazení:
f(x)
 1,
1,
g(x)
 g(x).
g(x).
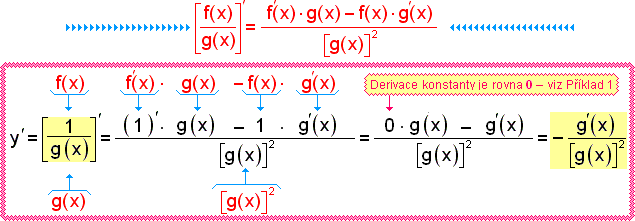
Potom z věty o derivaci podílu funkcí plyne pravidlo, které by bylo vhodné si zapamatovat a používat:
- Z věty V4 odvoďte pravidlo pro výpočet derivace v případě, že použijeme následující přiřazení:
f(x)
 k (k je libovolná reálná konstanta),
k (k je libovolná reálná konstanta),
g(x)
 g(x).
g(x).
|
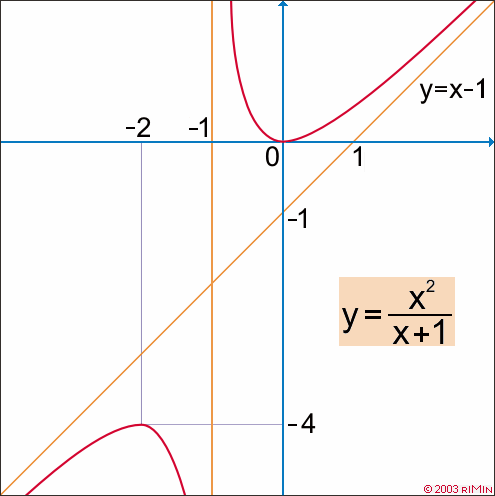
![]() v libovolném bodě x0 definičního oboru této funkce [to je množina všech reálných čísel kromě čísla - 1].
v libovolném bodě x0 definičního oboru této funkce [to je množina všech reálných čísel kromě čísla - 1].