J. Škrášek, Z. Tichý - Základy aplikované matematiky I
(historická poznámka ze strany 542)
Největším, vskutku revolučním dílem v historii matematiky je objev diferenciálního a integrálního počtu, zvaného souhrnně infinitezimální počet (od latinského slova infinitesimalis = nekonečně malý). Tento objev byl výsledkem dlouhodobého vývoje. Některé prvky infinitezimálního počtu se objevují už v pracích řeckých matematiků, např. v tzv. exhaustivní metodě Antiphonově (kolem r. 430 před n. l.), která se týká výpočtu obsahu plochy např. obsažené mezi kružnicí a pravidelným mnohoúhelníkem do ní vepsaným. Archimédes (kolem r. 225 před n. l.) používal při výpočtu objemů těles některých obratů, které představují jakousi integrační metodu.
Vydání Archimédových spisů v r. 1558 od Fedeica Commandina (1509 - 1575) mělo velký vliv na další vývoj infinitezimálních metod. Významná práce Johanna Keplera (1571 - 1630), zejména jeho spis "Nova stereometria doliorum vinariorum" (z roku 1615), tj. "Nové výpočty objemů vinařských sudů", práce Bonaventury Cavalieriho (asi 1598 - 1647) "Geometria indivisilibus continuorum" (1635), kde se opíral o scholastickou teorii "indivisibilií", podle níž vznikne pohybem bodu přímka, pohybem přímky rovina, a také práce Evangelisty Toricelliho (1608 - 1647) "Opera geometrica" (1644) podnítily mnoho matematiků v různých zemích ke studiu problémů, při jejichž řešení se používalo infinitezimálních veličin. Základní problémy se začaly zkoumat v obecnější formě. Kromě starých problémů určování obsahů a objemů (kvadratura a kubatura), popř. těžišť těles zde nabyl velkého významu problém tečny v daném bodě uvažované křivky. Při těchto zkoumáních se začaly uplatňovat zvláště dvě metody, geometrická a algebraická. Následovníci Cavalieriho, zejména Toricelli a Newtonův učitel Isaac Barrow (1630 - 1677) ve svém díle "Lectiones opticae et geometricae" (1669) a také Christian Huygens (1629 - 1695) ve svém díle "Horologium oscillatorium" (z roku 1665 a vydaném v roce 1673), používali řecké metody, spočívající na geometrických úvahách, aniž se přitom příliš starali o jejich přesnost. Jiní však, zvláště Pierre de Fermat (1601 - 1665), jeden z nejvýznačnějších předchůdců Newtonových, ve svém spise "Maxima at minima" (z roku 1629 až 1638), stejně jako René Descartes (1596 - 1650) ve svém díle "Géometrie" (z roku 1637) a John Wallis (1616 - 1703) v díle "Arithmetica infinitorum" (z roku 1655) zastupovali spíše protichůdný směr a používali při řešení těchto otázek metod nové algebry. Také Blaise Pascal (1623 - 1662) svým spisem "Traité général de la roulette" (1658) měl velký vliv zvláště na mladého Leibnize. Poznamenejme, že vedle Wallisovy knihy "Arithmetica infinitorum" obsahovala Huygensova kniha nejrozvinutější formu infinitezimálního počtu v době před Newtonem a Leibnizem. Dopisy i obě knihy Wallisovy a Huygensovy jsou plny nových poznatků o rektifikacích, obálkách soustavy a o kvadraturách.
Obecná metoda derivování a integrování mohla být nelezena jen člověkem, který ovládal nejen geometrické metody Řeků a Cavalieriho, ale i algebraickou metodu Fermatovu a Wallisovu. Takoví učenci se mohli proto vyskytnout až kolem roku 1660 a také se objevují v osobách Isaaca Newtona (1642 - 1727) a Gottfrieda Wilhelma Leibnize (1646 - 1716). O prioritě objevu infinitezimálního počtu bylo už mnohokrát psáno. Dnes ja jasně prokázáno, že oba učenci nalezli tyto obecné algoritmy nezávisle na sobě. Isaac Newton objevil infinitezimální počet jako prvý (v letech 1665 - 1666), kdežto Gottfried Wilhelm Leibniz asi o 10 let později, ale Leibniz své výsledky uveřejnil první (kolem roku 1685), zatím co Newton až v letech 1704 - 1736. Přitom Leibnizův výklad je podstatně elegantnější než Newtonův, takže velká část dnešní terminologie tohoto počtu byla přijata spíše od Leibnize než od Newtona.
Vlivem infinitezimálního počtu došlo k podstatným změnám v pojmech a metodách matematického myšlení. Do popředí matematických úvah se dostávají infinitezimální veličiny, přičemž se jejich použitím podařilo vyřešit mnoho fyzikálních a technických problémů, které byly do těch dob neřešitelné.
Mezi prvními šiřiteli infinitezimálního počtu brzy vynikli bratři Jacob Bernoulli (1654 - 1705) a Johann Bernoulli (1667 - 1748). Největší zásluhu o rozšíření a vybudování tohoto počtu si však získal švýcarský matematik Leonhard Euler (1707 - 1783), který většinu svého mimořádně plodného života prožil v Petrohradě jako člen tamější Akademie. Napsal přes 860 matematických a fyzikálních prací, jimiž přispěl významnými objevy téměř do všech oborů matematiky, které byly v tehdejší době pěstovány. Uveřejňoval své výsledky nejen v jednotlivých pojednáních rozličného rozsahu, ale i ve velkém počtu rozsáhlých učebnic, které poskytovaly v ucelené a systematické formě materiál nashromážděný během dřívějších dob, rozšířený mnoha jeho novými objevy. Jeho značná a všeobecně uznávaná autorita ustálila symboliku algebry a infinitezimálního počtu. Kromě knihy "Introductio in analysim ifinitorum" (z roku 1748) mělo velký ohlas jednak jeho dílo "Institutiones calculi integralis" (1768 - 1774), kde se nachází nejen výklad diferenciálního a integrálního počtu, ale i metody integrace diferenciálních rovnic, Eulerovy integrály prvního a druhého druhu (funkce beta a gama). Také variační počet, poprvé zpracovaný v jeho knize "Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes" (z roku 1744), obsahuje četné aplikace diferenciálních rovnic a mnoho nových výsledků o minimálních plochách. Dílo Eulerovo nemá v matematice téměř obdoby. Každý, kdo i dnes sáhne k jeho dílům, je plný obdivu k jeho jasnému myšlení a přesnému vyjadřování. Jeho latina je jasná, prostá a jeho použitá symbolika téměř moderní, neboť dnešní způsob označování matematických pojmů je téměř stejný jako Eulerův. Velcí matematikové téměř jednohlasně vyjadřovali svůj dluh vůči Eulerovi. Například Laplace říkal svým žákům:"Čtěte Eulera, je to učitel nás všech".A slavný C. F. Gauss prohlásil:"Studium Euleova díla zůstane nejlepší školou pro nejrůznější oblasti matematiky a nemůže je nic nahradit".
Z pozdějších matematiků, kteří podstaně přispěli k rozvoji infinitezimálního počtu, nejvíce vynikli Joseph Louis Lagrange (1736 - 1813), Pierre Simon Laplace (1749 - 1827), Adrien Marie Legendre (1752 - 1833), Jean Baptiste Joseph Fourier (1768 - 1830). Téměř všichni věnovali svou hlavní pozornost aplikacím matematiky na rozvíjející se tehdy průmyslovou výrobu.
Ani Euler se ve svých pracích nevyhnul chybám a nedostatkům, které pramenily hlavně z toho, že některé matematické pojmy nebyly dostatečně vyjasněny. Tal tomu např. bylo u nekonečných řad, kde nebyl vyjasněn pojem konvergence a upřesněna oprávněnost matematických operací s řadami. Proto se brzy ukázalo nutným, aby základy matematické analýzy byly polo ženy na přesný vědecký podklad. Na této práci se nejvíce podíleli Augustin Louis Cauchy (1789 - 1857), Karl Theodor Weierstrass (1815 - 1897), Bernard Bolzano (1781 - 1848), Thomas Jean Stieltjes (1856 - 1894), Henri Louis Lebesgue (1875 - 1941) a někteří další.
U nás k rozvoji infinitezimálního počtu nejvíce přispěli Matyáš Lerch (1860 - 1922), Karel Petr (1868 - 1950) a Vojtěch Jarník (1897 - 1970). První učebnici o infinitezimálním počtu (velmi elementární) zpracoval v roce 1864 Václav Šimerka (1819 - 1887) jako dodatek ke své učebnici "Algebra". Mnohem obsáhlejší byla učebnice (z roku 1871) od Františka Josefa Studničky (1836 - 1903). V současné době máme velmi zdařilé učebnice Vojtěcha Jarníka, a to dvojdílný "Diferenciální počet" a dvojdílný "Integrální počet", které vyšly již v několika vydáních.

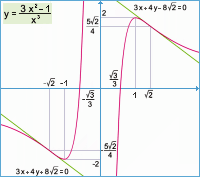
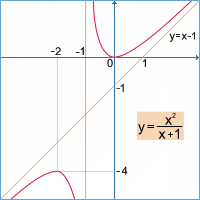

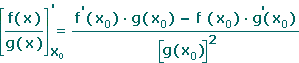 .
.