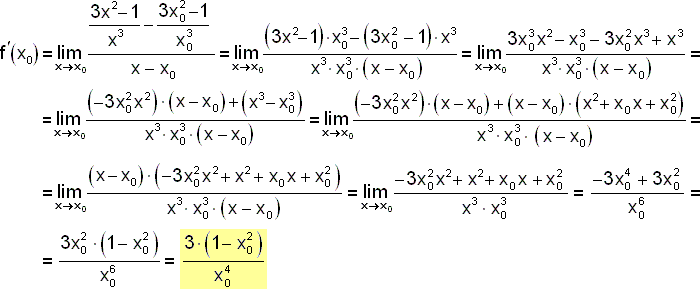|
Poznámky:
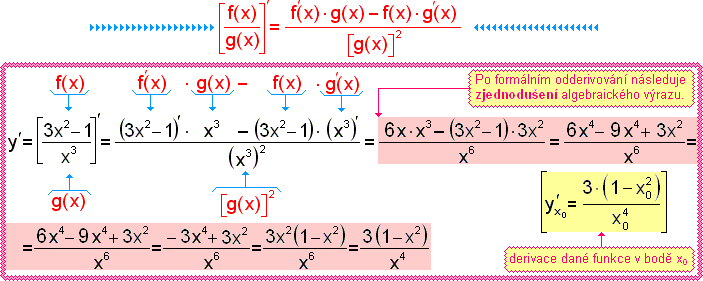
- Tento příklad názorně ukazuje to, že po odderivování následuje zjednodušení vypočítané derivace, to je vlastně zjednodušení algebraického výrazu. Zde budeme potřebovat následující znalosti:
roznásobení, vytýkání, rozklad na součin pomocí známých vzorců: a2-b2 = ...,
an-bn = ..., atd., krácení. V těchto úpravách bychom neměli dělat chyby, neboť zjednodušená derivace je opět začátkem následných výpočtů. Budeme například řešit následující úlohy:
 "urči, pro která x je první derivace dané funkce rovna nule",
"urči, pro která x je první derivace dané funkce rovna nule",
 "urči, pro která x je první derivace dané funkce kladná",
"urči, pro která x je první derivace dané funkce kladná",
 "urči, pro která x je první derivace dané funkce záporná",
"urči, pro která x je první derivace dané funkce záporná",
 "vypočítej derivaci první derivace dané funkce, tzv. druhou derivaci dané funkce", atd.
"vypočítej derivaci první derivace dané funkce, tzv. druhou derivaci dané funkce", atd.
- Prostudujte si další ilustrativní příklady.
|
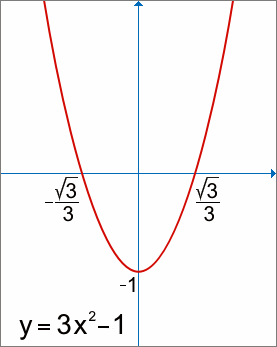
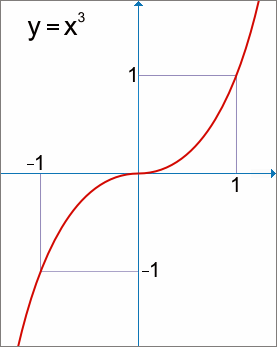
![]() [to je funkce
[to je funkce
![]() ].
Chceme vypočítat derivaci "nové" funkce v libovolném bodě x0 definičního oboru této funkce [to je množina všech reálných čísel kromě nuly].
].
Chceme vypočítat derivaci "nové" funkce v libovolném bodě x0 definičního oboru této funkce [to je množina všech reálných čísel kromě nuly].