Pythagoriáda 2002/2003 6. ročník

Pythagoriáda 2002/2003

6. ročník - školní kolo

1. příklad

Tři zedníci vyzdí za 3 dny 3 metry zdi. Kolik metrů zdi vyzdí za 6 dní šest zedníků? (Předpokládejte, že všichni pracují stejně rychle.)

2. příklad

Kolik trojúhelníků je na obrázku?

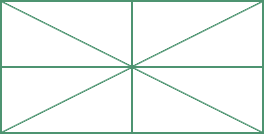3. příklad

Kolika způsoby lze zaplatit částku 350 Kč, máte-li k dispozici padesáti, sto a dvousetkorunové bankovky?

4. příklad

Těleso na obrázku je složeno ze stejných krychliček. Nakreslete co uvidíte, když se na toto těleso díváte shora.

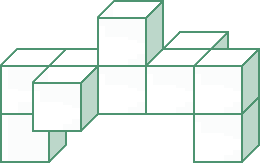5. příklad

Místo hvězdiček doplňte do součinu správné číslice.

6. příklad

Dvě prkna mají dohromady délku 14 m. První prkno je o 2 metry delší než druhé prkno. Jak jsou tato prkna dlouhá?

7. příklad

Mezi číslice umístěte znak sčítání (+) tak, aby součet takto vzniklých čísel byl 100.

1 2 3 4 5 6 7 = 100

8. příklad

Určete osu souměrnosti tohoto obrazce.

9. příklad

Od čísla MMDIX odečtěte číslo DX. Jejich rozdíl napište opět římskými číslicemi.

10. příklad

Z kolika nejméně a z kolika nejvíce krychliček může být složena tato stavba?

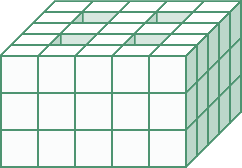11. příklad

Doplňte další tři členy řady tvořené podle určitého pravidla.

12. příklad

Ze kterého z uvedených obrázků nelze po vystřižení složit krychli?

A	B	C	D	E

13. příklad

V sáčku je 8 bílých a 7 zelených kuliček. Kolik nejméně kuliček musíte vytáhnout, abyste měli určitě alespoň 2 bílé a 4 zelené kuličky?

14. příklad

Na vydláždění podlahy haly tvaru obdélníku široké 3 m bylo zapotřebí 66 čtvercových dlaždic s délkou hrany 50 cm. Jak dlouhá je tato hala?

15. příklad

Ze dvou záhonů vzdálených od sebe 5 m lezou přímo proti sobě dva šneci. První leze rychlostí 8 cm/min, druhý leze rychlostí 7 cm/min. Jak daleko od sebe budou půl hodiny před tím, než se potkají?