Okruh 5    4 - 8 - 9
 9. Jsou dány paraboly P1: y2 = 1 – x a P2: y2 = - 4 ( x + 2 ). Napište rovnice jejich společných tečen.
 

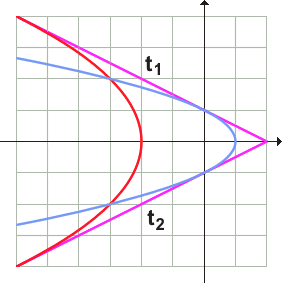
Společné tečny obou parabol se musí protínat na ose x v bodě např. K[a, 0]. Společná tečna bude určena rovnicí y = k x + l. Protože tato tečna musí procházet bodem K, musí platit rovnice y = k (x - a). Společná tečna musí mít s každou z daných parabol právě jeden společný bod. Musí tedy platit

(k x - k a)2 = 1 - x    (k x - k a)2 = - 4 (x + 2)
V každé z rovnic vypočítáme diskriminant a z podmínky D = 0 dostáváme soustavu:
4 k2 - 4 a k2 + 1 = 0    - 2 k2 - a k2 + 1 = 0.
Tato soustava má dvě řešení [k; a] = [0,5; 2] nebo [k; a] = [- 0,5; 2]. Existují dvě společné tečny daných parabol.
t1: y = - 0,5 x + 1,    t2: y = 0,5 x - 1
Čtvercová síť na obrázku je jednotková. Lze tedy zjistit např. souřadnice společných bodů obou parabol [-3, 2], [-3, -2] atd.

Gymnázium V. Hlavatého, Poděbradova 661, 440 62 Louny
© 2004 Milan Rieger - webdesign, grafika