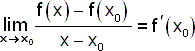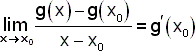Předpokládejme, že funkce f(x) a g(x) mají derivaci (vlastní) v bodě x₀. Potom má v bodě x₀ derivaci funkce f(x) . g(x) a platí:

[f(x) . g(x)]^'(x₀) = f^'(x₀) . g(x₀) + f(x₀) . g^'(x₀).

Důkaz:
Předpoklady věty:

1. Funkce f(x) má v bodě x₀ vlastní derivaci. To znamená, že existuje limita:
   
   
   
2. Funkce g(x) má v bodě x₀ vlastní derivaci. To znamená, že existuje limita:
   
   
   
3. Z předpokladu existence vlastní derivace funkce g(x) v bodě x₀, plyne spojitost funkce g(x) v bodě x₀. To ale znamená, že limita funkce g(x) v bodě x₀ je rovna hodotě funkce g(x) v bodě x₀ [u funkce f(x) platí ovšem totéž]. Symbolicky zapsáno tedy platí:
   
   
   

Pomocí definice derivace, "šikovných" úprav, vět o limitách funkcí a využitím uvedených předpokladů věty dostáváme:

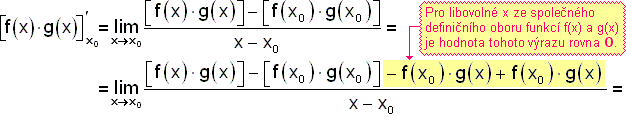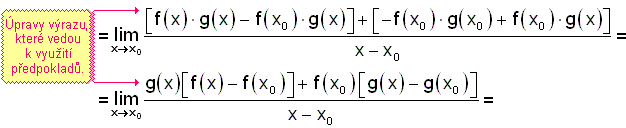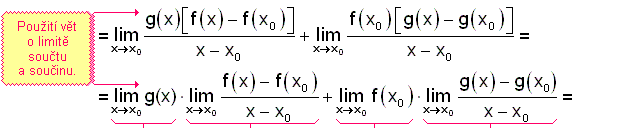Poznámky:

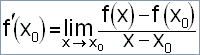
1. Podívejte se na ilustrativní příklady kliknutím na náhledech obrázků.