| 1. |
Jaký je nejmenší společný násobek čísel 8, 18, 21? |
| (A) |
(B) |
(C) |
(D) |
| 118 |
136 |
168 |
504 | |
| |
| 2. |
Které největší čtyřciferné číslo dělitelné 6 je možné sestavit z číslic 1, 4, 6, 7? (každou číslici lze použít jen jednou) |
| (A) |
(B) |
(C) |
(D) |
| 7 164 |
7 416 |
7 461 |
7 614 | |
| |
| 3. |
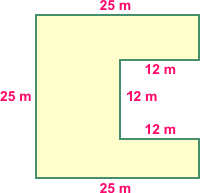
Jaký je obsah znázoněného obrazce? (všechny úhly jsou pravé)
| (A) |
(B) |
(C) |
(D) |
| 526 m2 |
498 m2 |
481 m2 |
465 m2 |
|
|
|
| |
| 4. |
V trojúhelníku ABC je poměr velikostí úhlů 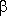 : :
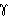 = 3 : 5.
Úhel = 3 : 5.
Úhel 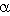 = 68°. Jaká je velikost úhlů = 68°. Jaká je velikost úhlů
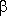 a a
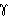 ? ?
|
| (A) |
(B) |
(C) |
(D) |
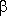 = 62°, = 62°, 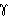 = 40° = 40° |
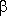 = 60°, = 60°, 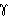 = 52° = 52° |
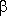 = 42°, = 42°, 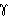 = 70° = 70° |
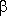 = 70°, = 70°, 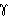 = 42° = 42° | |
| |
| 5. |
Jaký bude výsledek následujícího výpočtu? 84°17' - (26°42' + 35°39') = |
| (A) |
(B) |
(C) |
(D) |
| 21°56' |
21°6' |
22°16' |
23°17' | |
| |
| 6. |
Jaké měřítko má mapa, na které 13 cm představuje 9,75 km ve skutečnosti?
|
| (A) |
(B) |
(C) |
(D) |
| 1 : 17 500 |
1 : 75 000 |
1 : 175 000 |
1 : 1 750 000 | |
| |
| 7. |
Kterému z následujících výrazů je roven výraz 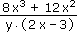 ? ? |
|
|
| |
| 8. |
Jestliže se cyklista pohybuje stálou rychlostí 36 km/h, kolik km ujede za 20 minut? |
| (A) |
(B) |
(C) |
(D) |
| 7,2 km |
12,0 km |
12.5 km |
13,6 km | |
| |
| 9. |
Bazén tvaru kvádru o rozměrech 50 m, 20 m a 17 dm je plný vody. Kolik 250litrových sudů be se vodou z bazénu zcela naplnilo? |
| (A) |
(B) |
(C) |
(D) |
| 680 |
952 |
6 800 |
9 520 | |
| |
| 10. |
V jaké vzdálenosti od sebe budou dvě tečny t1, t2 kružnice k (S; r = 4,2 cm), jestliže tyto tečny jsou navzájem rovnoběžné? |
| (A) |
(B) |
(C) |
(D) |
| |t1, t2| = 2r |
|t1, t2| = r |
|t1, t2| = 0,5 r |
Žádná z možností (A) až (C) není správná. | |
| |
| 11. |
Které číslo je řešením následujícího výpočtu? 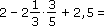 ? ? |
|
|
| |
| 12. |
Švadlenka Mirka ušije oblek za 4 dny, učnice Jitka za 6 dní. Jak dlouho potrvá šití obleku, budou-li na něm pracovat společně? (předpokládáme rovnoměrný výkon obou švadlen) |
| (A) |
(B) |
(C) |
(D) |
| 2 dny |
2,4 dne |
2,5 dne |
2 dny a 10 hodin | |
| |
| 13. |
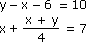 Jaké řešení má uvedená soustava rovnic?
Jaké řešení má uvedená soustava rovnic?
|
| (A) |
(B) |
(C) |
(D) |
| x = 18, y = 2 |
x = 5, y = 16 |
x = 2, y = 18 |
Soustava nemá řešení | |
| |
| 14. |
Skořápka ořechu tvoří 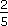 jeho hmotnosti. Kolik kg ořechů se musí rozlousknout, abychom vyloupali 1,5 kg jader? jeho hmotnosti. Kolik kg ořechů se musí rozlousknout, abychom vyloupali 1,5 kg jader? |
| (A) |
(B) |
(C) |
(D) |
| 2,5 kg |
2,6 kg |
2,7 kg |
2,9 kg | |
| |
| 15. |
Kolik % je 80 m2 ze 2,5 aru? |
| (A) |
(B) |
(C) |
(D) |
| 20 % |
32 % |
200 % |
320 % | |
| |
| 16. |
Které číslo je řešením následujícího příkladu? 0,136 . 103 + 621 . 10- 3 0,189 . 102 = |
| (A) |
(B) |
(C) |
(D) |
| -4, 679 |
0, 91 |
17, 92 |
117, 721 | |
| |
| 17. |
Kolik prvočísel je mezi prvními deseti přirozenými čísly? |
|
|
| |
| 18. |
Určete hodnotu číselného výrazu:
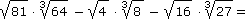
|
| (A) |
(B) |
(C) |
(D) |
| 36 |
24 |
20 |
16 | |
| |
| 19. |
Jaké je řešení následující rovnice? (x-3)2 - 1 = -3 (-2x + 1) + x2 - 1 |
| (A) |
(B) |
(C) |
(D) |
| x = 1 |
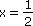 |
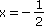 |
Rovnice má nekonečně mnoho řešení. | |
| |
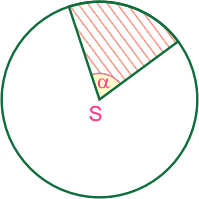
| 20. |
Kolik % plochy kruhu představuje vyšrafovaná část, jestliže vyznačený středový úhel
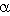 = 72° ? = 72° ?
| (A) |
(B) |
(C) |
(D) |
| 85 % |
40 % |
38 % |
20 % |
|
|
|
| |
| 21. |
|
Upravte následující výraz: 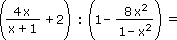
|
|
| |
| 22. |
|
Rychlost větru je 6 m/s. Kolik je to km/h?
| (A) |
(B) |
(C) |
(D) |
| 18,0 km/h |
21,6 km/h |
29,4 km/h |
216,0 km/h | |
|
| |
| 23. |
|
Která z následujících trojic čísel čísel může představovat délky stran pravoúhlého trojúhelníku?
| (A) |
(B) |
(C) |
(D) |
| 2, 3, 5 |
3, 5, 6 |
3, 4, 5 |
4, 5, 6 | |
|
| |
| 24. |
Jaký je obsah obdélníku, jehož úhlopříčka u = 1,5 dm a kratší strana měří 9 cm? |
| (A) |
(B) |
(C) |
(D) |
| 10,8 dm2 |
108 cm2 |
135 cm2 |
180 cm2 | |
| |
| 25. |
Jaký bude výsledek po úpravě následujícího zlomku? 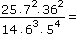
|
|
|
| |
| 26. |
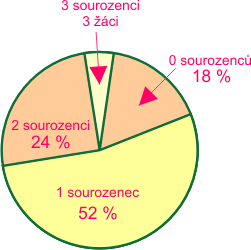
Statistickým šetřením byl zjišťován počet sourozenců u žáků 9. ročníku. Závěr byl zpracován kruhovým diagramem. Kolik žáků v 9. ročníku má jen jednoho sourozence?
| (A) |
(B) |
(C) |
(D) |
| 52 žáků |
46 žáků |
38 žáků |
26 žáků |
|
|
|
| |
| 27. |
V pravoúhlé soustavě souřadnic je sestrojena kružnice k se středem v bodě S = [4; 3], která prochází bodem A = [1; 3]. Určete souřadnice středu S' kružnice k' osově souměrné s kružnicí k podle osy o, která je shodná s osou y souřadného systému. |
| (A) |
(B) |
(C) |
(D) |
| S' = [-4; 3] |
S' = [4; 3] |
S' = [4; -3] |
S' = [3, -4] | |
| |
| 28. |
Cyklista vyjede z místa A v 8:00 stálou rychlostí 25 km/h. V 8:30 vyjíždí z místa A osobní auto stálou rychlostí 75 km/h po stejné trase. Kolik km celkem ujede cyklista, než ho osobní auto dostihne?
|
| (A) |
(B) |
(C) |
(D) |
| 15 km |
16,5 km |
17,25 km |
18,75 km | |
| |
| 29. |
Hmotnost nádoby s vodou je 3,1 kg. Kolik kg váží nádoba, když po odlití 20% vody je hmotnost nádoby se zbytkem vody 2,6 kg?
|
| (A) |
(B) |
(C) |
(D) |
| 0,5 kg |
0,6 kg |
0,68 kg |
1,1 kg | |
| |
| 30. |
Větší ozubené kolo se otočí za 4 minuty 72krát. Menší ozubené kolo se otočí za 6 minut 144krát. Jaký je poměr otáček za minutu menšího kola ku většímu kolu?
|
| (A) |
(B) |
(C) |
(D) |
| 1 : 2 |
2 : 1 |
4 : 3 |
5 : 4 | |
| |
|
Scio, obecně prospěšná společnost
Janovského 11
170 00 Praha 7
telefon: 266 711 522, fax: 266 711 524 |
| © 2004 Milan Rieger web
design, grafika |


