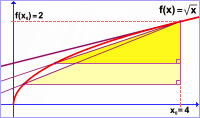
Pomocí definice derivace vypočítejte derivaci funkce v bodě x₀=1.

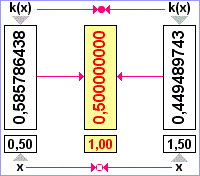
Uvědomíme si, že x₀=1, , f(x₀)=1. Dosazením do vzorce pro výpočet derivace dostaneme:

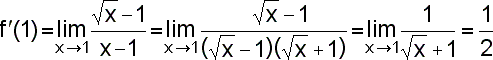
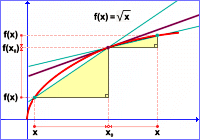
Pomocí definice derivace vypočítejte derivaci funkce v bodě x₀=4.

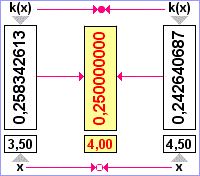
Platí x₀=4, , f(x₀)=2. Dosazením do vzorce pro výpočet derivace dostaneme:

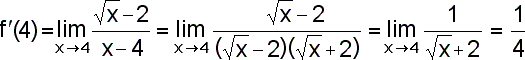
Pomocí definice derivace vypočítejte derivaci funkce v libovolném bodě x₀ z definičního oboru dané funkce.

Definičním oborem dané funkce je množina všech nezáporných reálných čísel. Tedy x₀ můžeme zvolit libovolně (pevně) z množiny nezáporných reálných čísel. Reálné číslo x je "pohyblivé" v tom smyslu, že se neomezeně přibližuje k číslu x₀. Vždy však platí, že čísla x₀, x jsou různá. Platí , . Výpočtem derivace podle definice dostáváme:

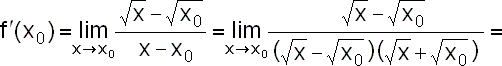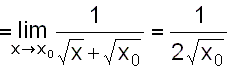
Porovnáme-li řešení první úlohy (x₀=1), druhé úlohy (x₀=4) a této obecné úlohy vidíme, že po dosazení do obecné úlohy za x₀=1 (x₀=4) dostáváme řešení první (druhé) úlohy. Vyplatí se zapamatování obecně dokázaného vzorce, který můžeme slovně formulovat takto: "Derivací druhé odmocniny je jedna polovina z převrácené hodnoty k druhé odmocnině".

Shrnutí a zobecnění: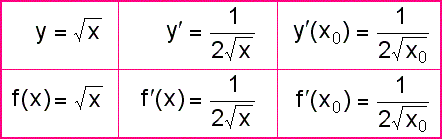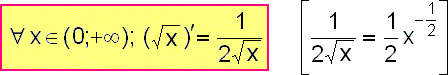
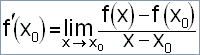
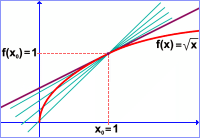