Pomocí definice derivace vypočítejte derivaci funkce v bodě x₀=1.

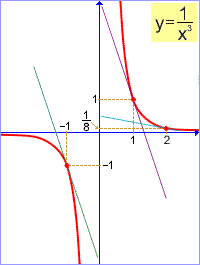
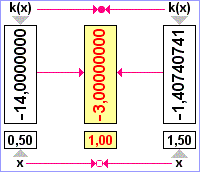
Uvědomíme si, že x₀=1, f(x₀)=1. Dosazením do vzorce pro výpočet derivace dostaneme:

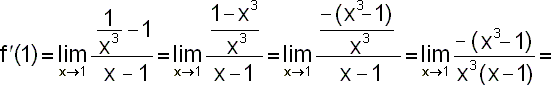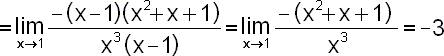
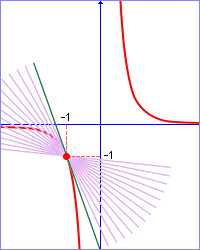
Pomocí definice derivace vypočítejte derivaci funkce v bodě x₀=-1.

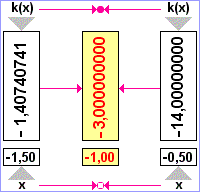
Platí x₀=-1, f(x₀)=-1. Dosazením do vzorce pro výpočet derivace dostaneme:

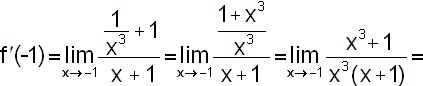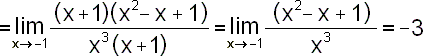
Pomocí definice derivace vypočítejte derivaci funkce v bodě x₀=2.

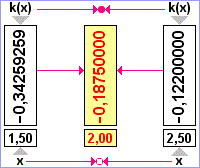
Platí x₀=2, Dosazením do vzorce pro výpočet derivace dostaneme:

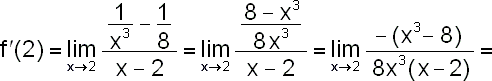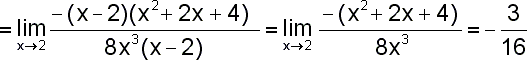
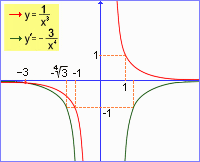
Pomocí definice derivace vypočítejte derivaci funkce v libovolném bodě x₀ z definičního oboru dané funkce.

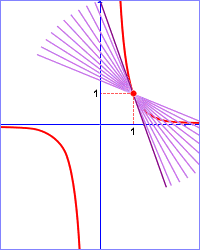
Definičním oborem dané funkce je množina všech reálných čísel kromě nuly. Tedy x₀ můžeme zvolit libovolně (pevně) z této množiny. Reálné číslo x je "pohyblivé" v tom smyslu, že se neomezeně přibližuje k číslu x₀. Vždy však platí, že čísla x₀, x jsou různá. Výpočtem derivace podle definice dostáváme: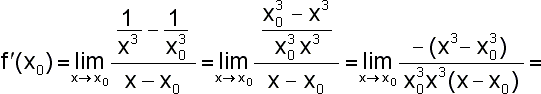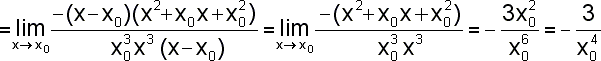

Shrnutí a zobecnění: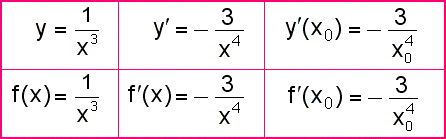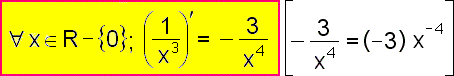
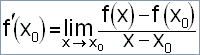