Pomocí definice derivace vypočítejte derivaci funkce v bodě x₀=2.

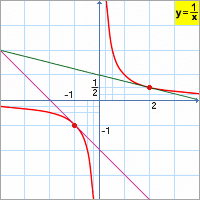
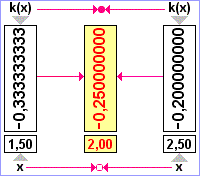
Uvědomíme si, že x₀=2, . Dosazením do vzorce pro výpočet derivace dostaneme:

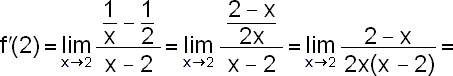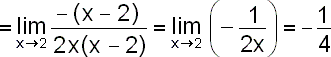
Pomocí definice derivace vypočítejte derivaci funkce v bodě x₀=-1.

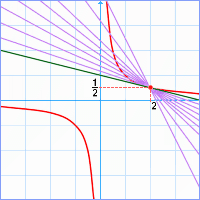
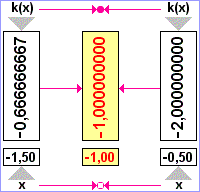
Platí x₀=-1, , f(-1)=-1. Dosazením do vzorce pro výpočet derivace dostaneme:

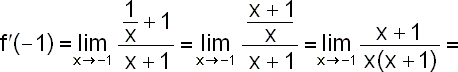Pomocí definice derivace vypočítejte derivaci funkce v libovolném bodě x₀ z definičního oboru dané funkce.

Definičním oborem funkce je množina všech reálných čísel kromě nuly. Tedy x₀ můžeme zvolit libovolně (pevně) z této množiny. Reálné číslo x je "pohyblivé" v tom smyslu, že se neomezeně přibližuje k číslu x₀. Vždy však platí, že čísla x₀, x jsou různá. Platí , . Výpočtem derivace podle definice dostáváme:

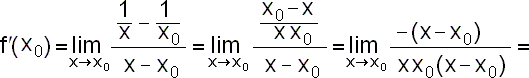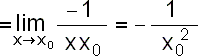
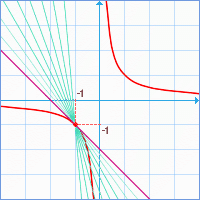
Porovnáme-li řešení první úlohy (x₀=2), druhé úlohy (x₀=-1) a této obecné úlohy vidíme, že po dosazení do obecné úlohy za x₀=2 (x₀=-1) dostáváme řešení první (druhé) úlohy.

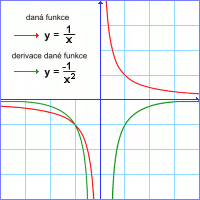
Shrnutí a zobecnění: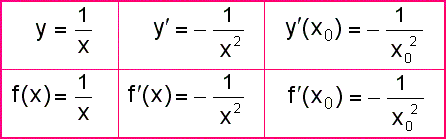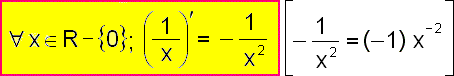
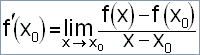