Příklad 5
|
Pomocí definice derivace vypočítejte derivaci funkce f: y=x4 v bodě x0=1. |
|||||||||
|
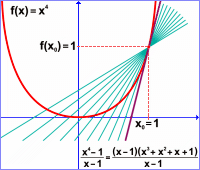
Uvědomíme si, že x0=1, f(x)=x4, f(x0)=1. Dosazením do vzorce pro výpočet derivace dostaneme: 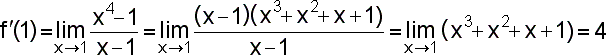
|
|||||||||
|
Pomocí definice derivace vypočítejte derivaci funkce f: y=x4 v bodě x0=-1. |
|||||||||
|
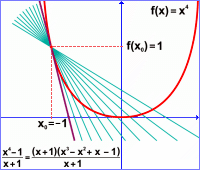
Platí x0=-1, f(x)=x4, f(x0)=1. Dosazením do vzorce pro výpočet derivace dostaneme: 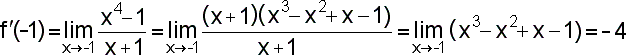
|
|||||||||
|
Pomocí definice derivace vypočítejte derivaci funkce f: y=x4 v libovolném bodě x0 z definičního oboru dané funkce. |
|||||||||
|
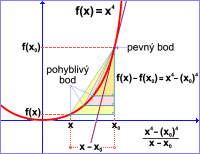
Definičním oborem dané funkce f: y=x4 je množina všech reálných čísel. Tedy x0 můžeme zvolit libovolně (pevně) z množiny reálných čísel. Reálné číslo x je "pohyblivé" v tom smyslu, že se neomezeně přibližuje k číslu x0. Vždy však platí, že čísla x0, x jsou různá. Platí f(x)=x2, f(x0)=(x0)2. Výpočtem derivace podle definice dostáváme: 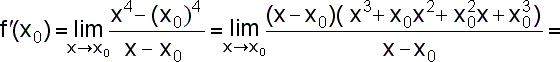 |
|||||||||
|
Porovnáme-li řešení první úlohy (x0=1) a této obecné úlohy vidíme, že po dosazení do obecné úlohy za x0=1 dostáváme řešení konkrétní úlohy. Vyplatí se zapamatování obecně dokázaného vzorce, který můžeme slovně formulovat takto: "Derivací funkce x na čtvrtou je funkce čtyři x na třetí". V matematice zapisujeme tento poznatek symbolicky (je to stručnější, přehlednější a jasnější) rovnicí y'=4x3 (zapisujeme-li rovnici funkce ve tvaru y=x4) nebo rovnicí f'(x)=4x3 (zapisujeme-li rovnici funkce ve tvaru f(x)=x4). Dále je nutné rozlišovat mezi derivací funkce v libovolném bodě definičního oboru dané funkce - to je funkce proměnné x. Derivací dané funkce v jednom bodě je reálné číslo. Vše je názorně shrnuto v následující tabulce: |
|||||||||
|
|||||||||
|
Zapsáno symbolicky: 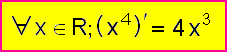
|
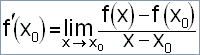
|
|
|
|
|
|
